If a function (continuos and twice differentiable) is always concave upward in an interval, then its graph lies always below the segment joining extremities of the graph in that interval and vice-versa.
Let f:R+→R+ is such that f(x)≥0∀x∈[a,b]. Then value of ∫baf(x)dx cannot exceed:
(f(a)+f(b))(b−a)3
(f(b)−f(a))(b−a)2
(f(b)+f(a))(b−a)2
None of the above
To solve the problem, we need to analyze the properties of the function f given that it is continuous, twice differentiable, and concave upward on the interval (a,b). We want to determine the maximum value of the integral ∫baf(x)dx.
1. Understanding Concavity:
Since f′′(x)≥0 for all x∈(a,b), this means that f is concave upward on the interval. A concave upward function lies below the line segment connecting its endpoints.
2. Graphical Representation:
Let's denote the points A=(a,f(a)) and B=(b,f(b)). The line segment joining these points can be represented as a straight line connecting A and B.
3. Area Under the Curve:
The integral ∫baf(x)dx represents the area under the curve of f(x) from x=a to x=b.
4. Trapezium Formation:
If we draw the line segment connecting A and B, we can visualize a trapezium formed by the curve f(x), the x-axis, and the line segment AB. The area under the curve f(x) will always be less than or equal to the area of this trapezium.
5. Calculating the Area of the Trapezium:
The area of the trapezium can be calculated using the formula for the area of a trapezium:
Area=12×(f(a)+f(b))×(b−a)
This is because the two parallel sides of the trapezium are f(a) and f(b), and the height is b−a.
6. Conclusion:
Therefore, the integral ∫baf(x)dx cannot exceed the area of the trapezium:
∫baf(x)dx≤12×(f(a)+f(b))×(b−a)
Final Answer:
The value of ∫baf(x)dx cannot exceed 12(f(a)+f(b))(b−a).
Since f′′(x)≥0 for all x∈(a,b), this means that f is concave upward on the interval. A concave upward function lies below the line segment connecting its endpoints.
Let's denote the points A=(a,f(a)) and B=(b,f(b)). The line segment joining these points can be represented as a straight line connecting A and B.
The integral ∫baf(x)dx represents the area under the curve of f(x) from x=a to x=b.
If we draw the line segment connecting A and B, we can visualize a trapezium formed by the curve f(x), the x-axis, and the line segment AB. The area under the curve f(x) will always be less than or equal to the area of this trapezium.
The area of the trapezium can be calculated using the formula for the area of a trapezium:
Area=12×(f(a)+f(b))×(b−a)
This is because the two parallel sides of the trapezium are f(a) and f(b), and the height is b−a.
Therefore, the integral ∫baf(x)dx cannot exceed the area of the trapezium:
∫baf(x)dx≤12×(f(a)+f(b))×(b−a)
The value of ∫baf(x)dx cannot exceed 12(f(a)+f(b))(b−a).
Topper's Solved these Questions
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise For Session 1
7 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise For Session 2
4 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
29 Videos
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
49 Videos
- PAIR OF STRAIGHT LINES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
Let a function f:R→R be defined as f(x)=x+sinx. The value of ∫2π0f−1(x)dx will be:
View SolutionLet f(x) be a differentiable function in the interval (0, 2) then the value of ∫20f(x)dx
View SolutionLet f(x) be a differentiable function on R such that f'(5−x)= f'(x)∀x∈[0,5] with f(0)=−10& f(5)=50,then the value of 5∫50f(x)dx
View SolutionIf f(x) is double differentiable function such that |f(x)|≤5 for each x in the interval [0,4] and f takes its largest value at an interior point of this interval , then value of |f'(0)|+|f''(4)| cannot be -
View SolutionLet f:R→R be a continuous function and f(x)=f(2x) is true ∀x∈R. If f(1)=3, then the value of ∫1−1f(f(x))dx is equal to
View SolutionThe value of the definite integral ∫10x dxx3+16 lies in the interval [a,b]. Then smallest such interval is
View SolutionLet a>0andf(x) is monotonic increase such that f(0)=0andf(a)=b,then ∫a0f(x)dx+∫b0f−1(x)dx is equal to
View SolutionLet f:R→R be a differentiable function and f(1)=4. Then, the value of limx→1∫f(x)42tx−1dt is :
View SolutionLet f(x) be a differentiable function and f(α)=f(β)=0(α<β), then the interval (α,β)
View Solution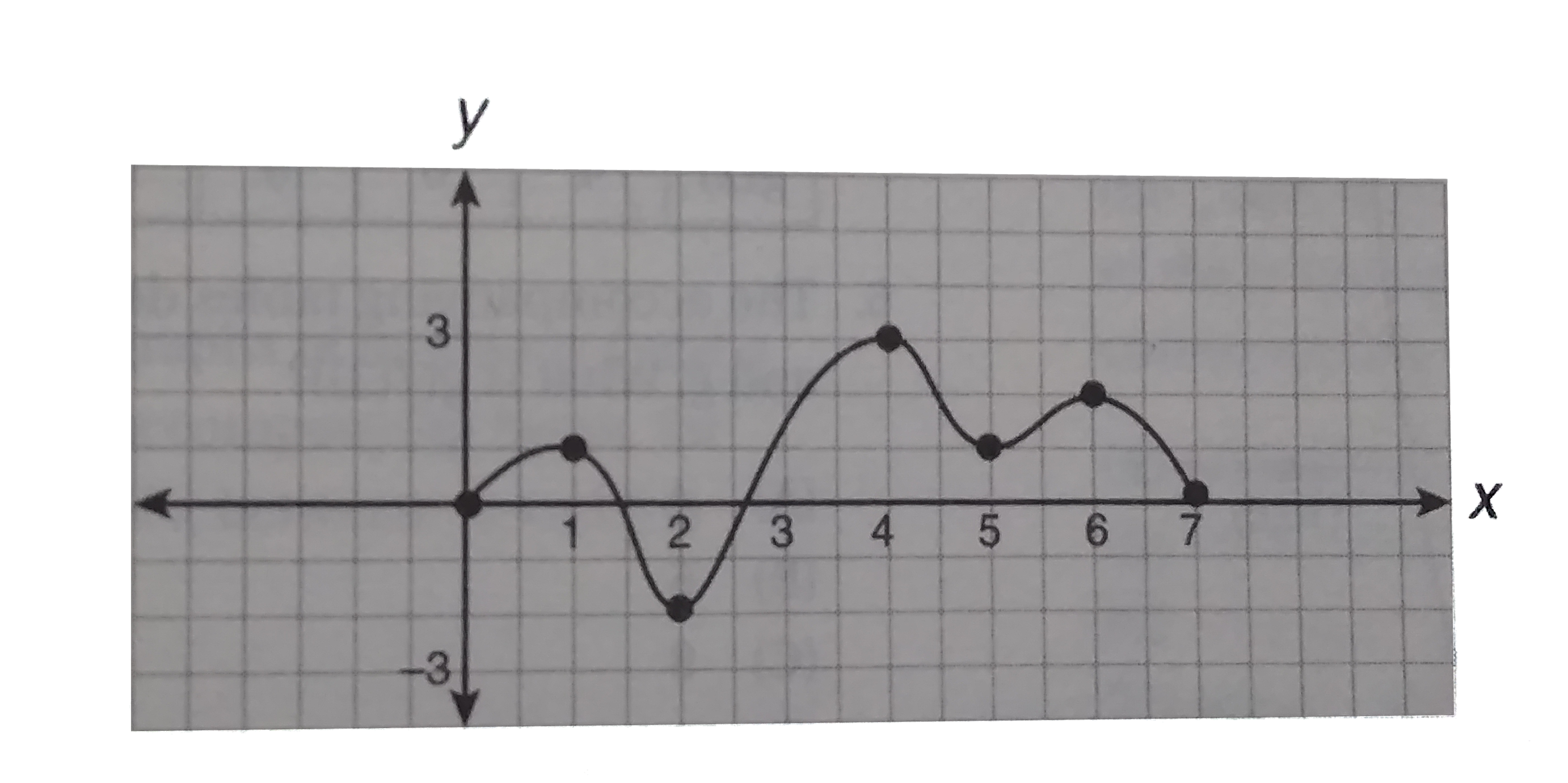
The graph above shows the function y=f(x) over the interval 0≤x≤7. What is the value of f(f(6))?
View Solution
