In cyclic quadrilateral ABCD, if and , then which of the following is (are) correct ?
The correct Answer is:A:D
To solve the problem, we will analyze the given information about the cyclic quadrilateral ABCD, where cotA=34 and tanB=−125. We will derive the necessary trigonometric values and check the correctness of the options provided.
Step 1: Find sinA and cosA
Given cotA=34, we can express this in terms of sine and cosine:
cotA=cosAsinA=34
Let sinA=4k and cosA=3k. Using the Pythagorean identity:
sin2A+cos2A=1
Substituting the values:
(4k)2+(3k)2=1⟹16k2+9k2=1⟹25k2=1⟹k2=125⟹k=15
Thus,
sinA=4k=45,cosA=3k=35
Step 2: Find sinB and cosB
Given tanB=−125, we can express this in terms of sine and cosine:
tanB=sinBcosB=−125
Let sinB=−12m and cosB=5m. Using the Pythagorean identity:
sin2B+cos2B=1
Substituting the values:
(−12m)2+(5m)2=1⟹144m2+25m2=1⟹169m2=1⟹m2=1169⟹m=113
Thus,
sinB=−12m=−1213,cosB=5m=513
Step 3: Find sinD
Since D=π−B in a cyclic quadrilateral, we have:
sinD=sin(π−B)=sinB=−1213
Step 4: Check the options
1. Option A: sinD=1213 (Incorrect, as we found sinD=−1213).
2. Option B: sinA+sinB=45−1213
sinA+sinB=4⋅13−12⋅565=52−6065=−865(Correct)
3. Option C: cosD=−513 (Correct, as D is in the second quadrant).
4. Option D: sinC−sinD
sinC=sinA=45andsinD=−1213
sinC−sinD=45+1213=52+6065=11265(Correct)
Final Results
- Correct Options: B, C, D
Given cotA=34, we can express this in terms of sine and cosine:
cotA=cosAsinA=34
Let sinA=4k and cosA=3k. Using the Pythagorean identity:
sin2A+cos2A=1
Substituting the values:
(4k)2+(3k)2=1⟹16k2+9k2=1⟹25k2=1⟹k2=125⟹k=15
Thus,
sinA=4k=45,cosA=3k=35
Given tanB=−125, we can express this in terms of sine and cosine:
tanB=sinBcosB=−125
Let sinB=−12m and cosB=5m. Using the Pythagorean identity:
sin2B+cos2B=1
Substituting the values:
(−12m)2+(5m)2=1⟹144m2+25m2=1⟹169m2=1⟹m2=1169⟹m=113
Thus,
sinB=−12m=−1213,cosB=5m=513
Since D=π−B in a cyclic quadrilateral, we have:
sinD=sin(π−B)=sinB=−1213
1. Option A: sinD=1213 (Incorrect, as we found sinD=−1213).
2. Option B: sinA+sinB=45−1213
sinA+sinB=4⋅13−12⋅565=52−6065=−865(Correct)
3. Option C: cosD=−513 (Correct, as D is in the second quadrant).
4. Option D: sinC−sinD
sinC=sinA=45andsinD=−1213
sinC−sinD=45+1213=52+6065=11265(Correct)
- Correct Options: B, C, D
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHS ENGLISHChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Statement I And Ii Type Questions)
Explore 11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHS ENGLISHChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Passage Based Questions)
Explore 13 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHS ENGLISHChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Single Option Correct Type Questions)
Explore 52 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBook:ARIHANT MATHS ENGLISHChapter:TRIGONOMETRIC EQUATIONS AND INEQUATIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 12 Videos
- VECTOR ALGEBRABook:ARIHANT MATHS ENGLISHChapter:VECTOR ALGEBRAExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 9 Videos
Similar Questions
Knowledge Check
In the figure, ABCD is a rectangle. The area of quadrilateral EBFD is one half the area of the rectangle ABCD. Which one of the following is the value of AD ?
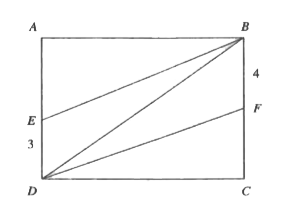 A5B6C7D12
A5B6C7D12
In cyclic quadrilateral ABCD (none of these being 90∘), which of the following is not true ?
View SolutionIn a cyclic quadrilateral ABCD, the value of 2+∑cosAcosB, is
View SolutionIn cyclic quadrilateral ABCD,∠A=3∠C and ∠D=5∠B. Find the measure of each angle of the quadrilateral.
View SolutionLet ABCD be a cyclic quadrilateral such that AB=2,BC=3,∠B=120∘ and area of quadrilateral =4√3. Which of the following is/are correct ?
View SolutionIn cyclic quadrilateral ABCD , AD = BC, ∠BAC=30∘and∠CBD=70∘ , find : angle ADC .
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily
View Solution