Let A, B, C represent the vertices of a triangle, where A is the origin and B and C have position b and c respectively.* Points M, N and P are taken on sides AB, BC and CA respectively, such that AMAB=BNBC=CPCA=α . If △ represent the area enclosed by the three vectors AN, BP and CM, then the value of α, for which △ is least
a. does not exist
b. 12
c. 14
d. None of these
The correct Answer is:B
To solve the problem step by step, we will analyze the triangle formed by the vectors and derive the area based on the given conditions.
Step 1: Define the points and vectors
Let the vertices of triangle ABC be:
- A = →0 (the origin)
- B = →b
- C = →c
Points M, N, and P are on sides AB, BC, and CA respectively such that:
- AMAB=BNBC=CPCA=α
Step 2: Express the position vectors of points M, N, and P
1. Position vector of M on side AB:
→M=(1−α)→0+α→b=α→b
2. Position vector of N on side BC:
→N=(1−α)→b+α→c
3. Position vector of P on side CA:
→P=(1−α)→c+α→0=(1−α)→c
Step 3: Find the vectors AN, BP, and CM
1. Vector AN:
→AN=→N−→A=((1−α)→b+α→c)−→0=(1−α)→b+α→c
2. Vector BP:
→BP=→P−→B=((1−α)→c)−→b=(1−α)→c−→b
3. Vector CM:
→CM=→M−→C=(α→b)−→c=α→b−→c
Step 4: Calculate the area of triangle formed by vectors AN, BP, and CM
The area of the triangle formed by vectors →AN,→BP,→CM can be calculated using the formula:
Area=12∣∣→AN×→BP∣∣
Step 5: Substitute the vectors into the area formula
Substituting the vectors into the area formula:
Area=12∣∣((1−α)→b+α→c)×((1−α)→c−→b)∣∣
Step 6: Simplify and find the minimum area
After simplifying the cross product and applying properties of determinants, we will find that the area can be expressed in terms of α.
Step 7: Minimize the area
To find the minimum area, we take the derivative of the area with respect to α and set it to zero:
d(Area)dα=0
Solving this will yield the value of α that minimizes the area.
Final Result
After performing the calculations, we find that the value of α that minimizes the area of triangle formed by vectors AN, BP, and CM is:
α=12
Let the vertices of triangle ABC be:
- A = →0 (the origin)
- B = →b
- C = →c
- AMAB=BNBC=CPCA=α
1. Position vector of M on side AB:
→M=(1−α)→0+α→b=α→b
→N=(1−α)→b+α→c
→P=(1−α)→c+α→0=(1−α)→c
1. Vector AN:
→AN=→N−→A=((1−α)→b+α→c)−→0=(1−α)→b+α→c
→BP=→P−→B=((1−α)→c)−→b=(1−α)→c−→b
→CM=→M−→C=(α→b)−→c=α→b−→c
The area of the triangle formed by vectors →AN,→BP,→CM can be calculated using the formula:
Area=12∣∣→AN×→BP∣∣
Substituting the vectors into the area formula:
Area=12∣∣((1−α)→b+α→c)×((1−α)→c−→b)∣∣
After simplifying the cross product and applying properties of determinants, we will find that the area can be expressed in terms of α.
To find the minimum area, we take the derivative of the area with respect to α and set it to zero:
d(Area)dα=0
Solving this will yield the value of α that minimizes the area.
After performing the calculations, we find that the value of α that minimizes the area of triangle formed by vectors AN, BP, and CM is:
α=12
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 1
12 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 2
18 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
Let A, B, C respresent the vertices of a triangle, where A is the origin and B and C have position b and c respectively. Points M, N and P are taken on sides AB, BC and CA respectively, such that (AM)/(AB)=(BN)/(BC)=(CP)/(CA)=alpha Q. AN+BP+CM is
View SolutionThevertices of a triangle ABC are A(−7,8),B(5,2)andC(11,0). If D, E, F are the mid-points of the sides BC,CAandAB respectively, show that ΔABC=4ΔDEF.
View SolutionBC is an equilateral triangle. A circle is drawn with centre A so that it cuts AB and AC at points M and N respectively. Prove that BN = CM
View SolutionIn a triangle ABC , let P and Q be points on AB and AC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC show that the BDCD=CEAE=AFBF=−1
View SolutionA line L intersects three sides BC, CA and AB of a triangle in P,Q,R respectively, show that BPPC.CQQA.ARRB=−1
View SolutionIf A,B,C represents the three sides of an equilateral triangle taken in the same order then find the angle between i) A and B ii) B and C iii) A and C.
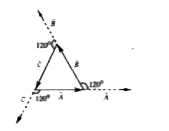
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
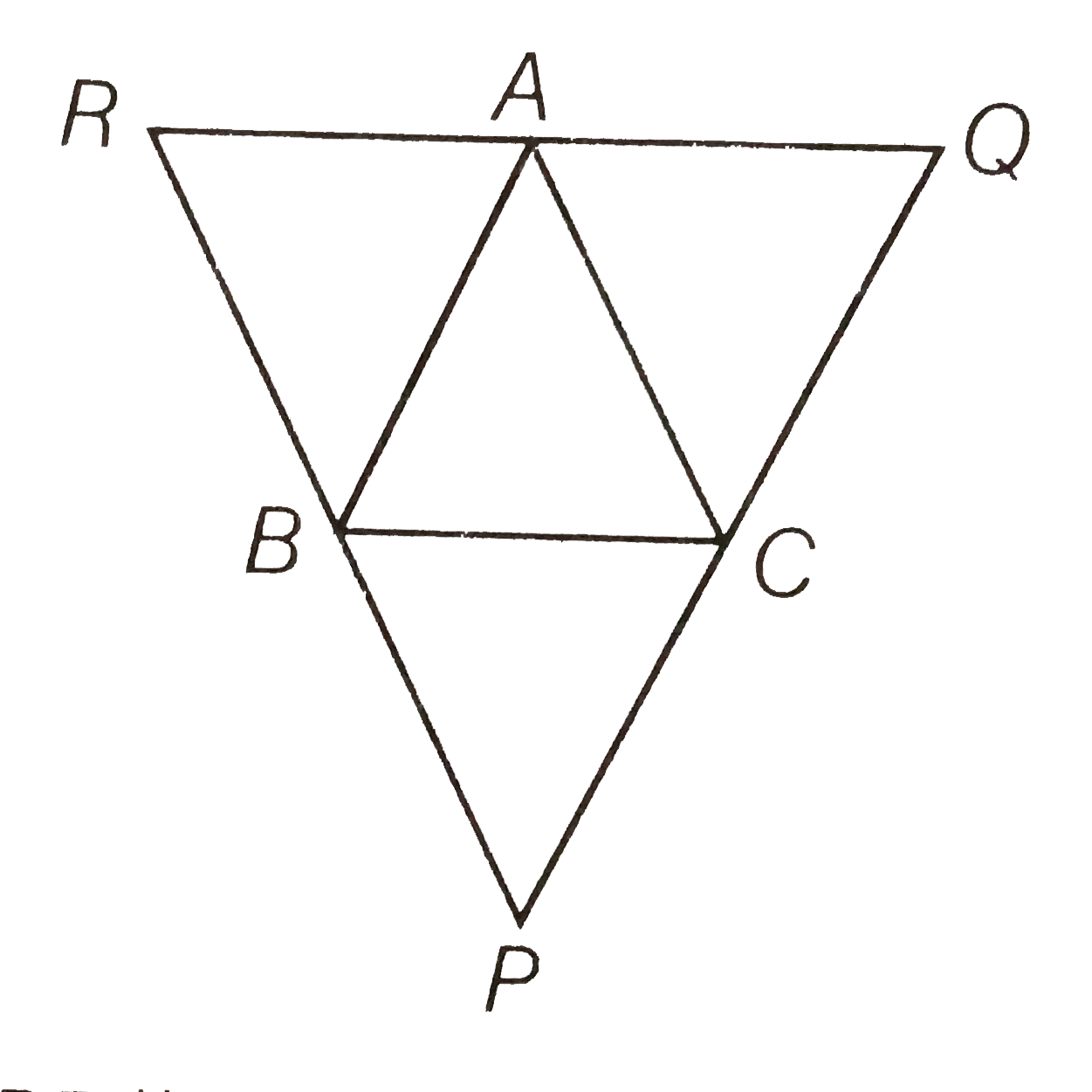
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View Solution
