Show that the radius of closed right circular cylinder of given surface area maximum volume is equal to half of its height.

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for Show that the radius of closed right circular cylinder of given surface area maximum volume is equal to half of its height. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The height and radius of the right circular cylinder below are given in meters. What is the volume, in cubic meters, of the cylinder?
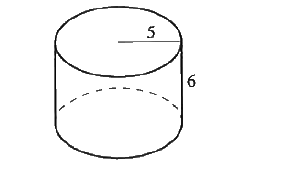    ocr_image

    A30π
    B31π
    C150π
    D180π