Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM= CN. Prove that BMDN is a parallelogram.
Step by step video & image solution for Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM= CN. Prove that BMDN is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - QUADRILATERALS AND ITS PROPERTIES - 4 MARKS QUESTIONS
7 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - POLYGONS - 4 MARKS QUESTIONS
4 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
E and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionTwo points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BY. Prove that □AXCY is a parallelogram.
View SolutionM and N are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CN is parallel to AM.
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP.
View SolutionProve that the diagonals of a parallelogram bisect each other.
View SolutionE is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD . Prove that AEFD is a parallelogram.
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:
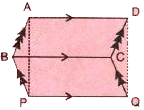
APQD is a parallelogram
View SolutionX and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Prove that □AXCY is a parallelogram.
View SolutionThe vector −2ˆi+4ˆj+4ˆkand−4ˆi−4ˆk represent the diagonals BD and AC of a parallelogram ABCD. Then, find the area of the parallelogram.
View Solution
