In the given AB=BC=DCand∠AOB=50∘
∠BOD
The correct Answer is:100∘
To solve the problem step by step, we will use the properties of angles and equal sides in the context of circles.
1. Identify Given Information:
- We are given that AB=BC=DC.
- We are also given that ∠AOB=50∘.
2. Understand the Implications of Equal Sides:
- Since AB=BC, the angles opposite these equal sides must also be equal. Therefore, ∠AOB=∠BOC.
- Similarly, since BC=DC, we have ∠BOC=∠COD.
3. Set Up the Equal Angles:
- From the above, we can conclude:
- ∠BOC=∠AOB=50∘
- ∠COD=∠BOC=50∘
4. Calculate Angle BOD:
- The angle ∠BOD is the sum of angles ∠BOC and ∠COD:
∠BOD=∠BOC+∠COD
- Substituting the values we found:
∠BOD=50∘+50∘=100∘
5. Final Answer:
- Therefore, ∠BOD=100∘.
- We are given that AB=BC=DC.
- We are also given that ∠AOB=50∘.
- Since AB=BC, the angles opposite these equal sides must also be equal. Therefore, ∠AOB=∠BOC.
- Similarly, since BC=DC, we have ∠BOC=∠COD.
- From the above, we can conclude:
- ∠BOC=∠AOB=50∘
- ∠COD=∠BOC=50∘
- The angle ∠BOD is the sum of angles ∠BOC and ∠COD:
∠BOD=∠BOC+∠COD
- Substituting the values we found:
∠BOD=50∘+50∘=100∘
- Therefore, ∠BOD=100∘.
Topper's Solved these Questions
Similar Questions
In the given AB=BC=DCand∠AOB=50∘
∠AOC
View SolutionIn the given AB=BC=DCand∠AOB=50∘
∠AOD
View SolutionIn the given figure, AB = BC = DC and ∠AOB=50∘

∠AOC =?
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠OAC
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOC
View SolutionIn the given figure, AB = DB and AC = DC. If ∠ABD=58∘,∠DBC=(2x−4)∘,∠ACB=y+15∘and∠DCB=63∘, find the values of x and y.
View SolutionIn the given figure, find ∠AOB.

View SolutionIn the given figure, AC = AE, AB = AD and ∠BAD=∠EAC. Show that : BC = DE.

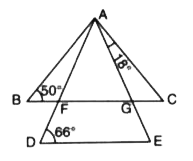
View SolutionIn the following figure , AB = BC and AD = DE.
if ∠B=50∘,∠D=66∘and∠GAC=18∘ find the measure of angles DAE, BAF and AGF.
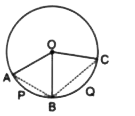
View SolutionIn the given figure , arc APB : arc BQC = 2: 3 and ∠AOC=150∘, Find :
(i) ∠AOB
(ii) ∠BOC
(iii) ∠OBA
(iv) ∠OCB
(v) ∠ABC
View Solution
