In the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOC
The correct Answer is:∠BOC=40∘
To solve the problem, we need to find the measure of angle BOC given that arc AB is twice arc BC and angle AOB is 80 degrees.
1. Understand the Given Information:
- We know that ∠AOB=80∘.
- We also know that arc AB is twice arc BC, which can be written as:
arc AB=2×arc BC
2. Use the Property of Angles and Arcs:
- The angle subtended by an arc at the center of the circle is proportional to the length of the arc. Therefore, we can write:
∠AOB=2×∠BOC
- This means that the angle AOB is twice the angle BOC.
3. Substitute the Known Value:
- We know that ∠AOB=80∘. Thus, we can substitute this value into the equation:
80∘=2×∠BOC
4. Solve for Angle BOC:
- To find ∠BOC, we divide both sides of the equation by 2:
∠BOC=80∘2=40∘
5. Conclusion:
- Therefore, the measure of angle BOC is 40∘.
Final Answer:
∠BOC=40∘
- We know that ∠AOB=80∘.
- We also know that arc AB is twice arc BC, which can be written as:
arc AB=2×arc BC
- The angle subtended by an arc at the center of the circle is proportional to the length of the arc. Therefore, we can write:
∠AOB=2×∠BOC
- This means that the angle AOB is twice the angle BOC.
- We know that ∠AOB=80∘. Thus, we can substitute this value into the equation:
80∘=2×∠BOC
- To find ∠BOC, we divide both sides of the equation by 2:
∠BOC=80∘2=40∘
- Therefore, the measure of angle BOC is 40∘.
∠BOC=40∘
Topper's Solved these Questions
Similar Questions
In the given arc AB= twice are BC and ∠AOB=80∘ find:
∠OAC
View SolutionIn the given AB=BC=DCand∠AOB=50∘
∠BOD
View SolutionIn the given AB=BC=DCand∠AOB=50∘
∠AOC
View SolutionIn the given AB=BC=DCand∠AOB=50∘
∠AOD
View SolutionIn the given figure,AB is parallel to DC. ∠BCE=80∘and∠BAC=25∘.F∈d:(i) angle CAD <br>(ii) angle CBD <br>(iii) angle ADC
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
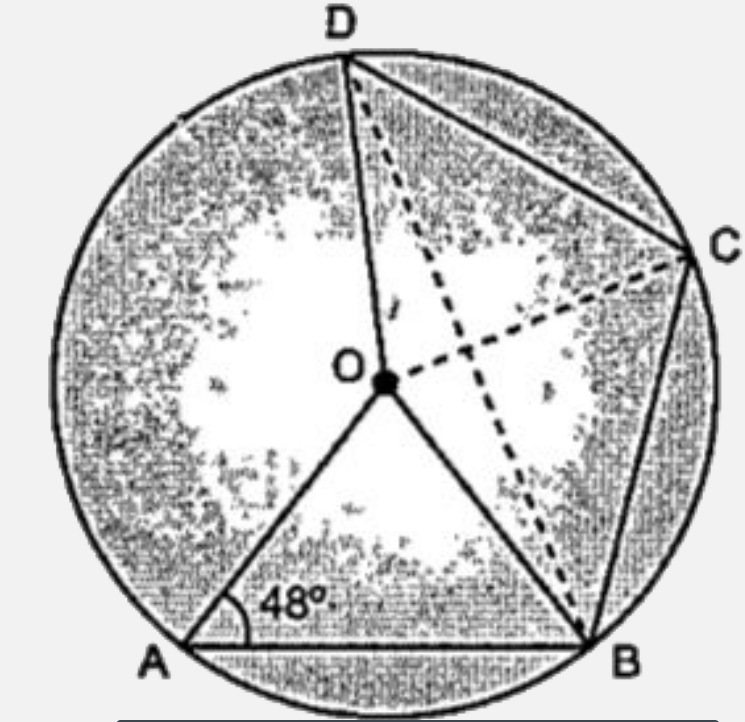
∠OBD
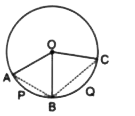
View SolutionIn the given figure , arc APB : arc BQC = 2: 3 and ∠AOC=150∘, Find :
(i) ∠AOB
(ii) ∠BOC
(iii) ∠OBA
(iv) ∠OCB
(v) ∠ABC
View SolutionIn the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.
if ∠AOB=100∘ find ∠BOC
View SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED

View SolutionIn the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠BOC
View Solution
