The following figure shows a solid of uniform cross-section. Find the volume of the solid.
All measurements are in centimetres. Assume that all angles in the figure are right angles.
The correct Answer is:
To find the volume of the solid with a uniform cross-section, we will break it down into two cuboids and calculate their individual volumes before summing them up.
1. Identify the Dimensions of the First Cuboid:
- Length (L1) = 9 cm
- Breadth (B1) = 4 cm
- Height (H1) = 3 cm
2. Calculate the Volume of the First Cuboid:
- The formula for the volume of a cuboid is:
Volume=Length×Breadth×Height
- Substituting the dimensions:
Volume of First Cuboid=L1×B1×H1=9×4×3
- Calculating:
9×4=36
36×3=108 cm3
3. Identify the Dimensions of the Second Cuboid:
- Length (L2) = 4 cm
- Breadth (B2) = 6 cm
- Height (H2) = 3 cm
4. Calculate the Volume of the Second Cuboid:
- Using the same volume formula:
Volume of Second Cuboid=L2×B2×H2=4×6×3
- Calculating:
4×6=24
24×3=72 cm3
5. Calculate the Total Volume of the Solid:
- Add the volumes of both cuboids:
Total Volume=Volume of First Cuboid+Volume of Second Cuboid
Total Volume=108 cm3+72 cm3=180 cm3
Final Answer:
The volume of the solid is 180 cm3.
---
- Length (L1) = 9 cm
- Breadth (B1) = 4 cm
- Height (H1) = 3 cm
- The formula for the volume of a cuboid is:
Volume=Length×Breadth×Height
- Substituting the dimensions:
Volume of First Cuboid=L1×B1×H1=9×4×3
- Calculating:
9×4=36
36×3=108 cm3
- Length (L2) = 4 cm
- Breadth (B2) = 6 cm
- Height (H2) = 3 cm
- Using the same volume formula:
Volume of Second Cuboid=L2×B2×H2=4×6×3
- Calculating:
4×6=24
24×3=72 cm3
- Add the volumes of both cuboids:
Total Volume=Volume of First Cuboid+Volume of Second Cuboid
Total Volume=108 cm3+72 cm3=180 cm3
The volume of the solid is 180 cm3.
Topper's Solved these Questions
- MENSURATION (PLANE FIGURE) BOOK - ICSECHAPTER - MENSURATION (PLANE FIGURE) EXERCISE - TOPIC-3 (4 Marks Questions)
8 Videos
- MENSURATION (PLANE FIGURE) BOOK - ICSECHAPTER - MENSURATION (PLANE FIGURE) EXERCISE - TOPIC-2 (4 Marks Questions )
7 Videos
- MEAN AND MEDIANBOOK - ICSECHAPTER - MEAN AND MEDIANEXERCISE - Exercise 19(C)
36 Videos
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(B)
23 Videos
Similar Questions
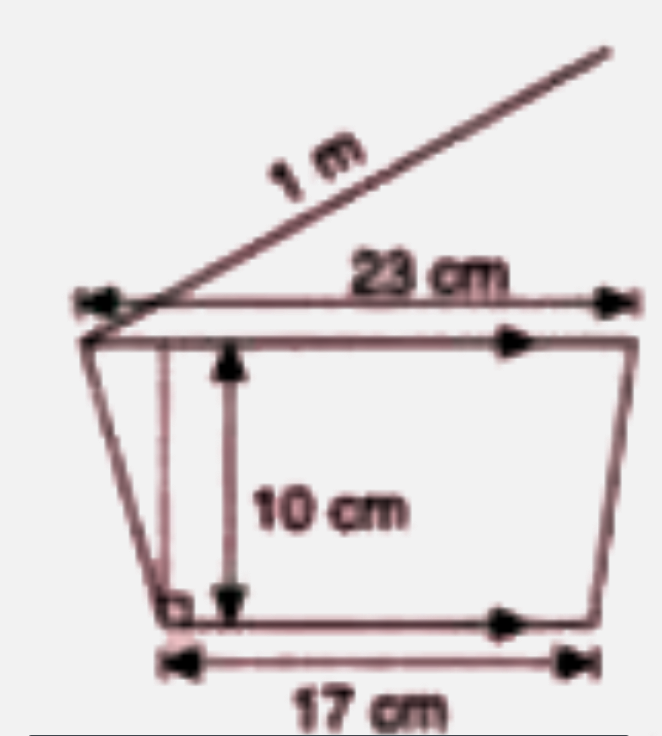
The adjoining figure shows a solid of uniform cross-section whch is a trapezium in shape. If the length of the solid is 1m, find its volume
View SolutionFind ∠A in the given figure.

View SolutionIn the given figure, find ∠ABC.

View SolutionIn the given figure, find ∠AOB.

View SolutionFind all the angles of an equilateral triangle.
View SolutionFind ∠AOB in the given figure.

View SolutionFind the measure of ∠x in the adjoining figure.

View SolutionWhich of the following figures represets the cross-section of an octahedral site?
View SolutionFigure shows a long wire bent at the middle to from a right angle

View SolutionFind the angle measure x in the following figures.
View Solution
