Use the following figure to find :
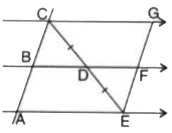
BC, if AB = 7.2 cm.
The correct Answer is:7.2 cm
Step by step video, text & image solution for Use the following figure to find : BC, if AB = 7.2 cm. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Book:ICSEChapter:MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Exercise:EXERCISE 12(A)
Explore 23 Videos
- MENSURATION (PLANE FIGURE) Book:ICSEChapter:MENSURATION (PLANE FIGURE) Exercise:TOPIC-3 (4 Marks Questions)
Explore 8 Videos
- MID-POINT THEOREMBook:ICSEChapter:MID-POINT THEOREMExercise:4 MARKS QUESTION
Explore 15 Videos
Similar Questions
In the following figure, XY is parallel to BC,AX=9cm,XB=4.5cmandBC=18cm.
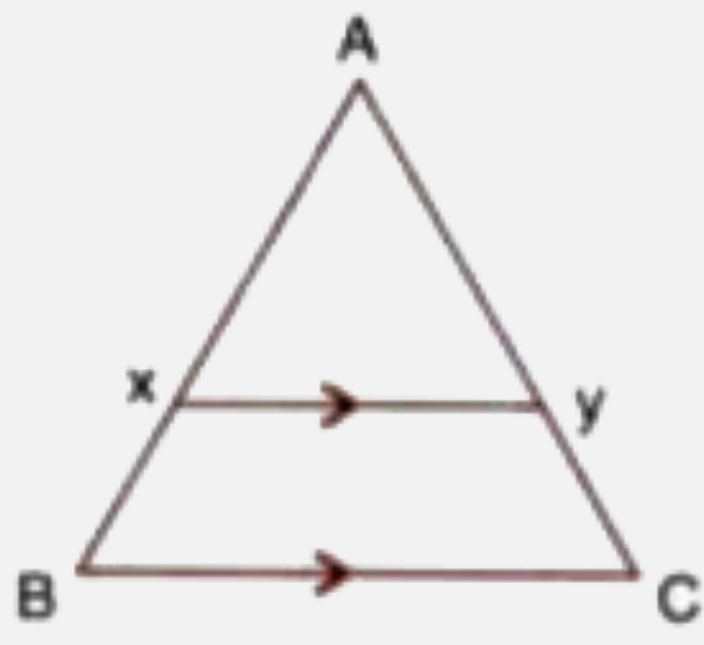
XY
View SolutionIn the following figure:
OA=2cm
=AB=2BC=12CD=16DE Find the length of OE.

View SolutionIn the following figure, ∠ABC=90∘ AB = (x+8) cm , BC = (x+ 1) cm and AC = (x+15) cm.
Find the lengths of the sides of the triangles.

View SolutionIn the following figure, point D divides AB in the ratio 3: 5. Find :

Also if :
BC = 4.8 cm, find the length of DE.
View SolutionIn the following figure, point D divides AB in the ratio 3: 5. Find :
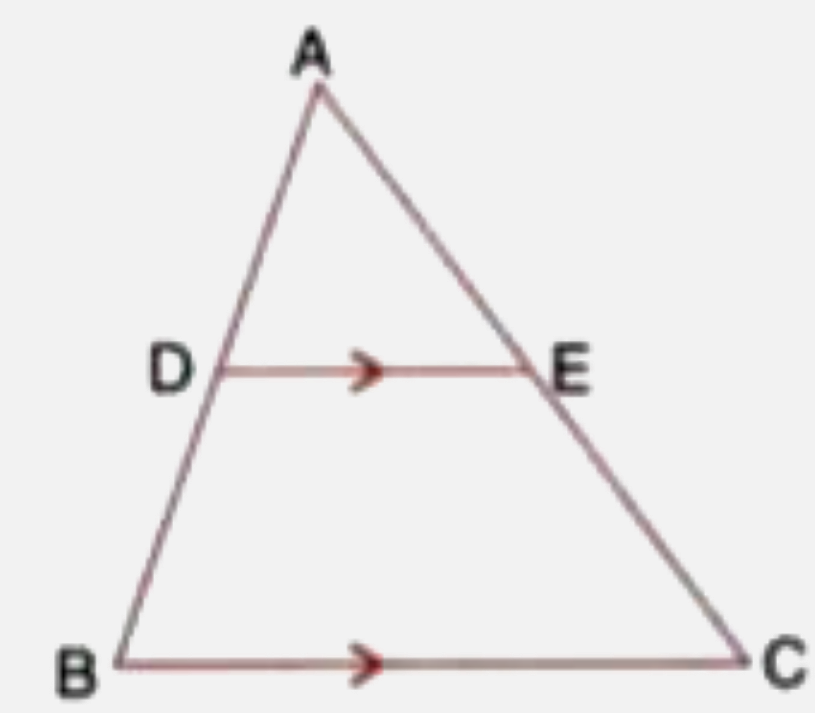
Also, if:
DE = 24 cm, find the length of BC.
View SolutionIn the following figure , AB = BC , AD ⊥BCandCE⊥AB.prove that AD = CE
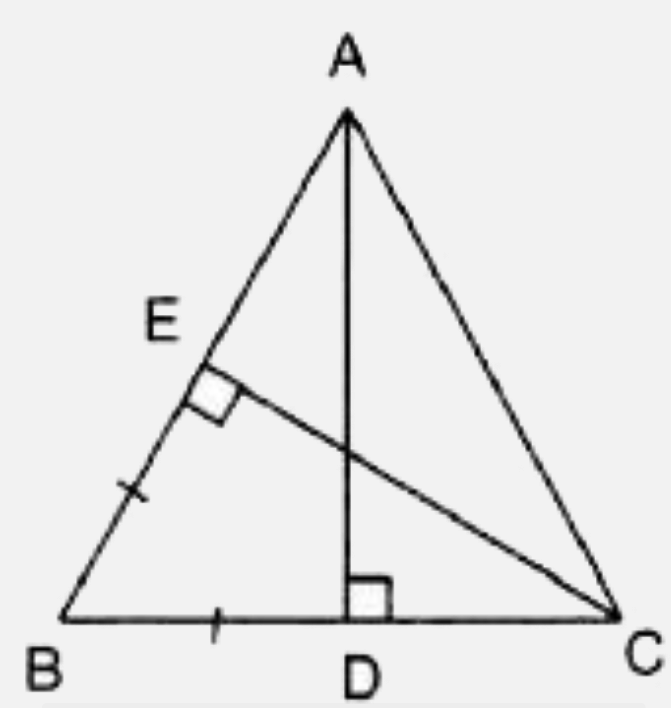
View SolutionFind the area of the quadrilateral ABCD , given in the adjoining figure in which AB = 14 cm , BC = 78 cm , CD = 112 cm BD = 50 cm and DA = 48 cm .

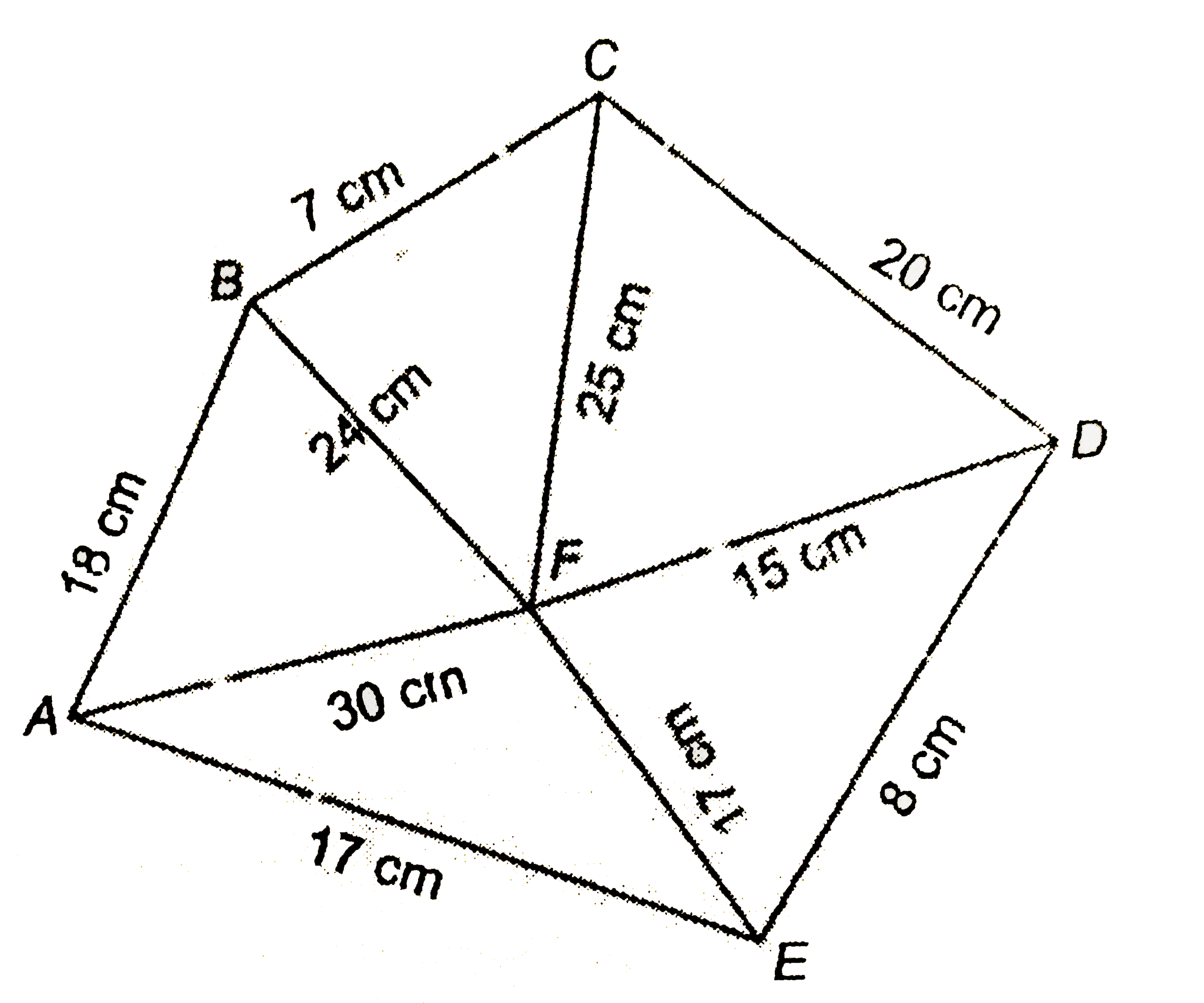
View SolutionFind the area of the given figure
Given AB = 18 cm, BC = 7 cm, CD = 20 cm, DE = 8 cm, EA = 17 cm, AF = 30 cm, BF = 24 cm, CF = 25 cm, FD = 15 cm, EF = 17 cm.
View SolutionIn the following figure, AD is perpendicular to BC and D divides BC in the ration 1 : 3.
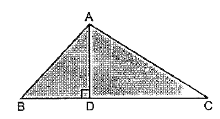
Prove that : 2AC2=2AB2+BC2
View SolutionUsing a rular and compass only :
(i) Construct a triangle ABC with the following data :
AB = 3.5 cm, BC = 6 cm and ∠ABC=120∘.
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circunference of the circle which is equidistant from AB and BC.
(iii) Measure ∠BCP.
View Solution