A kite is attached to a 100 m long string. Find the greatest height reached by the kite when its string makes an angle of 60∘ with the travel round.
The correct Answer is:86.6 m
To find the greatest height reached by the kite when its string makes an angle of 60∘ with the ground, we can use trigonometric principles. Here’s a step-by-step solution:
Step 1: Understand the problem
We have a kite attached to a 100 m long string, and the string makes an angle of 60∘ with the horizontal ground. We need to find the vertical height (h) of the kite above the ground.
Step 2: Visualize the scenario
Draw a right triangle where:
- The hypotenuse (the string) is 100 m.
- The angle with the horizontal (ground) is 60∘.
- The height (h) is the opposite side to the angle 60∘.
Step 3: Use the sine function
In a right triangle, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. Therefore, we can write:
sin(60∘)=oppositehypotenuse=h100
Step 4: Substitute the known values
We know that sin(60∘)=√32. Substituting this into the equation gives:
√32=h100
Step 5: Solve for h
To find h, we can rearrange the equation:
h=100⋅√32
Calculating this gives:
h=50√3
Step 6: Calculate the numerical value
Using the approximate value of √3≈1.732:
h≈50⋅1.732≈86.6 m
Conclusion
The greatest height reached by the kite is approximately 86.6 meters.
---
We have a kite attached to a 100 m long string, and the string makes an angle of 60∘ with the horizontal ground. We need to find the vertical height (h) of the kite above the ground.
Draw a right triangle where:
- The hypotenuse (the string) is 100 m.
- The angle with the horizontal (ground) is 60∘.
- The height (h) is the opposite side to the angle 60∘.
In a right triangle, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. Therefore, we can write:
We know that sin(60∘)=√32. Substituting this into the equation gives:
To find h, we can rearrange the equation:
Using the approximate value of √3≈1.732:
The greatest height reached by the kite is approximately 86.6 meters.
Topper's Solved these Questions
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -4 ( COMPLEMENTARY ANGLES ) (3 MARKS QUESTIONS )
7 Videos
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -4 ( COMPLEMENTARY ANGLES ) (4 MARKS QUESTIONS )
4 Videos
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -3 ( SOLUTION OF RIGHT TRIANGLES ANGLES ) (3 MARKS QUESTIONS )
6 Videos
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(C)
118 Videos
Similar Questions
A kite is attached to a string. Find the length of the string , when the height of the kite is 60 m and the string makes an angle 30∘ with the ground .
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
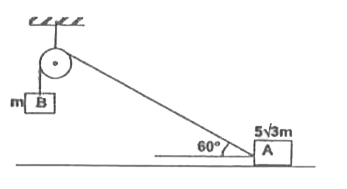
View SolutionA block A of mass 5√3m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
View SolutionA simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angel of 370 with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.

View SolutionA particle of mass 100 g, is made to describe a vertical circle of radius 1 m. Its instantaneous speed is 1ms−1 when the string makes an sngle of 30∘ with the vertical Find the tension in the string at this position. Can the particle complete its circular path? (g=10ms−2)
View SolutionA bullet is fired with speed 50m/s at 45∘ angle with horizontal. Find the height of the bullet when its direction of motion makes angle 30∘ with the horizontal.
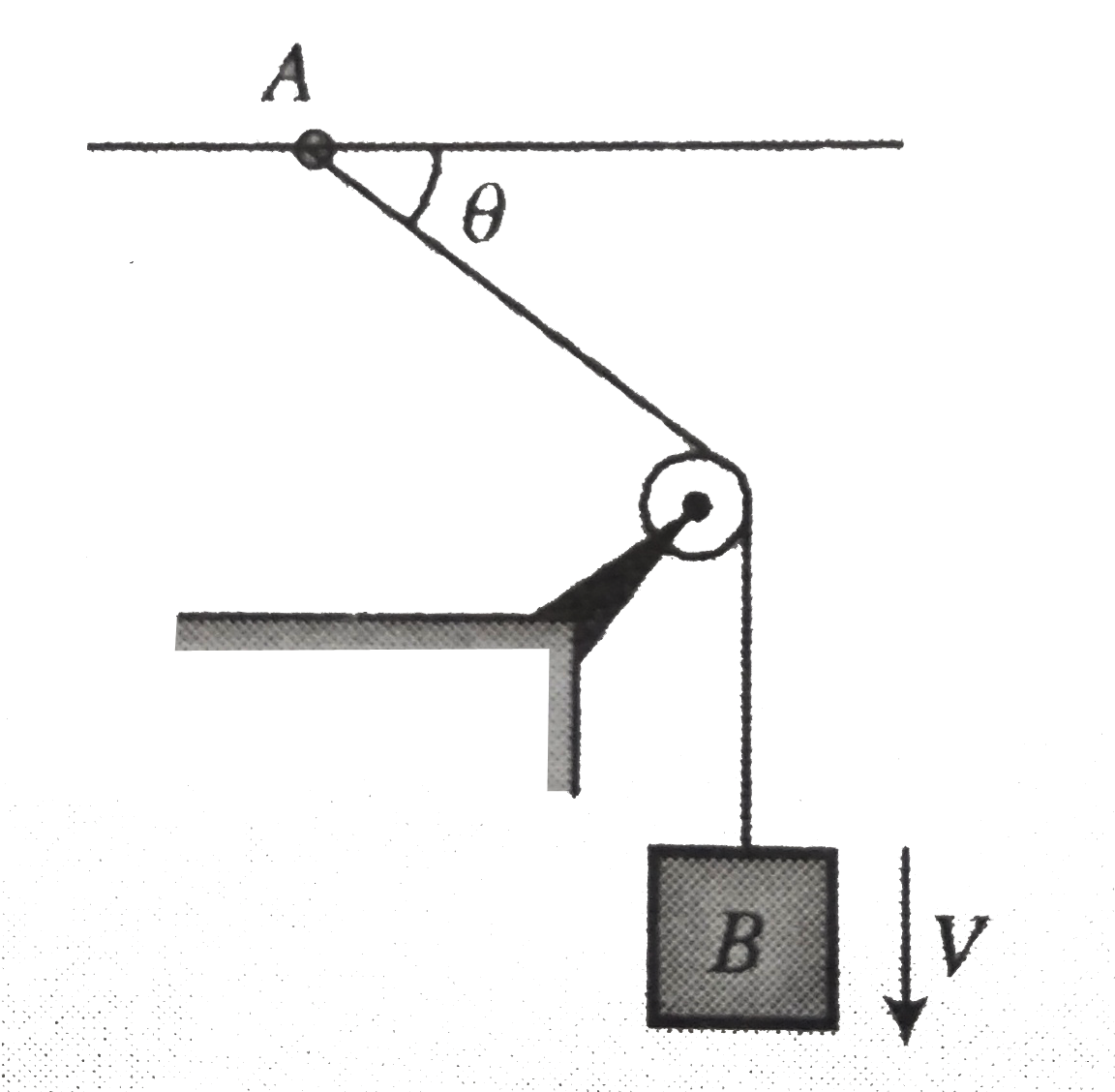
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
View SolutionThe bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
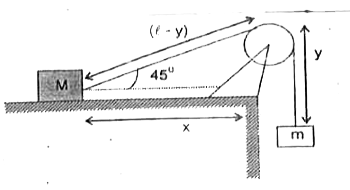
View SolutionTwo masses M and m are connected by a light inextensible string which passes over a small pulley as shown in the diagram. If the mass m is moving downward with a velocity v when the string makes an angle of 45∘ with the horizontal, find the total K.E. of the two masses. AsSigmae that the mass M moves horizontally.
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View Solution
