A mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
(a)Mg√2
(b)Mg(√2−1)
(c)Mg(√2+1)
(d)Mg√2
The correct Answer is:B
To solve the problem, we need to find the horizontal force required to displace a mass M suspended by a weightless string until the string makes an angle of 45∘ with the vertical. Let's break down the solution step by step.
Step 1: Understand the Forces Acting on the Mass
When the mass is displaced to make an angle of 45∘ with the vertical, two main forces act on the mass:
1. The gravitational force Fg=Mg acting downward.
2. The tension T in the string acting along the string.
Step 2: Draw a Free Body Diagram
Draw a diagram showing the mass at an angle of 45∘. Label the forces:
- The weight Mg acting downward.
- The tension T acting along the string.
- The horizontal force F that we need to find.
Step 3: Resolve the Forces
When the string makes an angle of 45∘:
- The vertical component of the tension T must balance the weight:
Tcos(45∘)=Mg
- The horizontal component of the tension provides the centripetal force:
Tsin(45∘)=F
Step 4: Use Trigonometric Values
Since cos(45∘)=sin(45∘)=1√2, we can rewrite the equations:
1. From the vertical balance:
T⋅1√2=Mg⇒T=Mg√2
2. Substitute T into the horizontal force equation:
F=T⋅1√2=(Mg√2)⋅1√2=Mg
Step 5: Conclusion
Thus, the horizontal force required to displace the mass until the string makes an angle of 45∘ with the vertical is:
F=Mg
Final Answer
The required horizontal force is F=Mg.
---
When the mass is displaced to make an angle of 45∘ with the vertical, two main forces act on the mass:
1. The gravitational force Fg=Mg acting downward.
2. The tension T in the string acting along the string.
Draw a diagram showing the mass at an angle of 45∘. Label the forces:
- The weight Mg acting downward.
- The tension T acting along the string.
- The horizontal force F that we need to find.
When the string makes an angle of 45∘:
- The vertical component of the tension T must balance the weight:
Tcos(45∘)=Mg
- The horizontal component of the tension provides the centripetal force:
Tsin(45∘)=F
Since cos(45∘)=sin(45∘)=1√2, we can rewrite the equations:
1. From the vertical balance:
T⋅1√2=Mg⇒T=Mg√2
2. Substitute T into the horizontal force equation:
F=T⋅1√2=(Mg√2)⋅1√2=Mg
Thus, the horizontal force required to displace the mass until the string makes an angle of 45∘ with the vertical is:
F=Mg
The required horizontal force is F=Mg.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE)80videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS2videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
A mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60∘ with the vertical is
View SolutionA body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
View SolutionResolve horizontally and vertically a force f =8 N which makes an angle of 45∘ with the horizontal.
View SolutionResolve horizontally and vertically a force F=8N which makes an angle of 45∘ with the horizontal.
View SolutionResolve horizontally and vertically a force F=8N which makes an angle of 45∘ with the horizontal.
View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
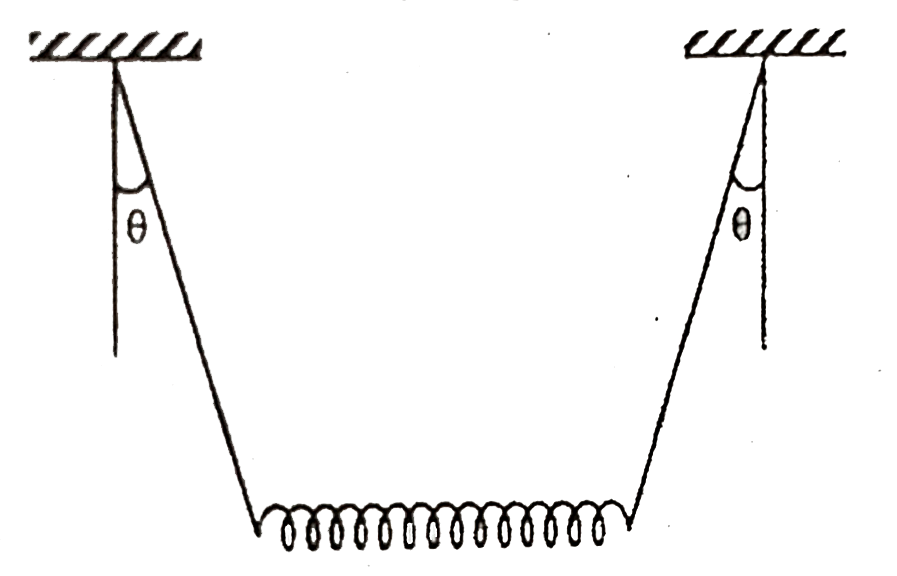 View Solution
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.
 View Solution
View Solution

