(a) Show that the velocity of the centre of mass of a moving isolated system remains constant.
To show that the velocity of the center of mass of a moving isolated system remains constant, we can follow these steps:
Step 1: Define an Isolated System
An isolated system is defined as a system where no external forces are acting on it. This means that the net external force acting on the system is zero.
Step 2: Use the Equation of Motion
According to Newton's second law, the net external force (Fnet) acting on a system is equal to the mass (m) of the system multiplied by the acceleration (a) of the center of mass:
Fnet=m⋅a
Step 3: Apply the Condition of an Isolated System
For an isolated system, since there are no external forces acting on it, we have:
Fnet=0
Step 4: Relate Force to Acceleration
Substituting this condition into the equation of motion gives us:
0=m⋅a
Step 5: Analyze the Implications
Since the mass m of the system is not zero, we can conclude that the acceleration a of the center of mass must also be zero:
a=0
Step 6: Conclude About Velocity
If the acceleration of the center of mass is zero, it implies that the velocity of the center of mass is constant. This means that if the system was initially moving, it will continue to move with that same constant velocity.
Final Conclusion
Thus, we have shown that the velocity of the center of mass of a moving isolated system remains constant.
---
An isolated system is defined as a system where no external forces are acting on it. This means that the net external force acting on the system is zero.
According to Newton's second law, the net external force (Fnet) acting on a system is equal to the mass (m) of the system multiplied by the acceleration (a) of the center of mass:
Fnet=m⋅a
For an isolated system, since there are no external forces acting on it, we have:
Fnet=0
Substituting this condition into the equation of motion gives us:
0=m⋅a
Since the mass m of the system is not zero, we can conclude that the acceleration a of the center of mass must also be zero:
a=0
If the acceleration of the center of mass is zero, it implies that the velocity of the center of mass is constant. This means that if the system was initially moving, it will continue to move with that same constant velocity.
Thus, we have shown that the velocity of the center of mass of a moving isolated system remains constant.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-D6videos
SELF ASSESSMENT PAPER 3
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-B13videos
SELF ASSESSMENT PAPER 3
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-D (Answer the following )6videos
SELF ASSESSMENT PAPER 02
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 4EXERCISE - Section-D6videos
SELF ASSESSMENT PAPER 4
Similar Questions
Knowledge Check
- Question 1 - Select One
The velocity of centre of mass of the system remains constant, if the total external force acting on the system is.
Aa. minimumBb. maximumCc. unityDd. zero
Calculate centre of mass of the system
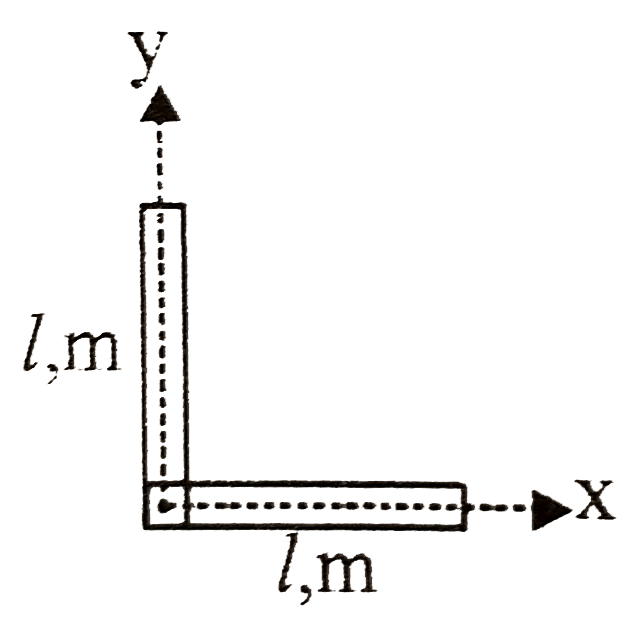 View Solution
View SolutionStatement-1: if there is no external torque on a body about its centre of mass, then the velocity of the center of mass remains constant.
Statement-2: The linear momentum of an isolated system remains constant.View SolutionAs observed in the laboratory system , a 6 MeV proton is incident on a stationary 12 C target. The velocity of centre of mass of the system is (Take mass of proton to be 1 amu)
View SolutionAnswer the following:
(a) Write the expression for the force →F acting on a particle of mass m and charge q moving with velocity→V in a magnetic field →B . Under what conditions will it move in
(i) a circular path and (ii) a helical path ?
(b) Show that the kinetic energy of the particle moving a magnetic field remains constant.View SolutionThe co-ordinates of the centre of mass of the system as shown in figure are
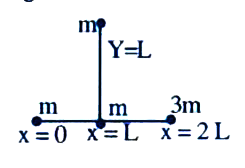 View Solution
View SolutionPredict the change in internal energy for an isolated system at constant volume.
View SolutionFor an isolated system, the entropy :
View Solution

