As observed in the laboratory system , a 6 MeV proton is incident on a stationary 12 C target. The velocity of centre of mass of the system is (Take mass of proton to be 1 amu)
2.6×106ms−1
6.2×106ms−1
10×106ms−1
10ms−1
The correct Answer is:A
To find the velocity of the center of mass of the system when a 6 MeV proton is incident on a stationary 12 C target, we can follow these steps:
Step 1: Identify the masses and energies
- Mass of the proton, m1=1amu
- Mass of the carbon target, m2=12amu
- Kinetic energy of the proton, KE=6MeV
Step 2: Convert kinetic energy to joules
1 MeV = 1.6×10−13J
So,
KE=6MeV=6×1.6×10−13J=9.6×10−13J
Step 3: Calculate the velocity of the proton
Using the kinetic energy formula:
KE=12mv2
We can rearrange this to find the velocity v:
v=√2×KEm1=√2×9.6×10−131.66×10−27
(Note: 1amu=1.66×10−27kg)
Calculating this gives:
v≈√1.92×10−121.66×10−27≈√1.157×1015≈1.075×107m/s
Step 4: Calculate the velocity of the center of mass
The velocity of the center of mass vcm is given by:
vcm=m1v1+m2v2m1+m2
Since the carbon target is stationary, v2=0:
vcm=m1v1+0m1+m2=m1v1m1+m2
Substituting the values:
vcm=(1amu)×(1.075×107m/s)1amu+12amu=1.075×10713≈8.27×105m/s
Final Answer
The velocity of the center of mass of the system is approximately 8.27×105m/s.
---
- Mass of the proton, m1=1amu
- Mass of the carbon target, m2=12amu
- Kinetic energy of the proton, KE=6MeV
1 MeV = 1.6×10−13J
KE=6MeV=6×1.6×10−13J=9.6×10−13J
Using the kinetic energy formula:
KE=12mv2
We can rearrange this to find the velocity v:
v=√2×KEm1=√2×9.6×10−131.66×10−27
(Note: 1amu=1.66×10−27kg)
v≈√1.92×10−121.66×10−27≈√1.157×1015≈1.075×107m/s
The velocity of the center of mass vcm is given by:
vcm=m1v1+m2v2m1+m2
Since the carbon target is stationary, v2=0:
vcm=m1v1+0m1+m2=m1v1m1+m2
vcm=(1amu)×(1.075×107m/s)1amu+12amu=1.075×10713≈8.27×105m/s
The velocity of the center of mass of the system is approximately 8.27×105m/s.
Similar Questions
Knowledge Check
The velocity of centre of mass of the system remains constant, if the total external force acting on the system is.
Aa. minimumBb. maximumCc. unityDd. zeroCentre of mass of three particles of masses 1kg,2kgand3kg lies at the point (1,2,3) and centre of mass of another system of particles 3kgand2kg lies at the point (−1,3,−2). Where should we put a particle of mass 5kg so that the centre of mass of entire system lies at the centre of mass of first system ?
A(0, 0, 0)B(1, 3, 2)C(-1, 2, 3)D(3, 1, 8)
In the earth-moon system, if T1 and T2 are period of revolution of earth and moon respectively about the centre of mass of the system them
View SolutionThre identical masses are kept at the corners of an equilateral triangle ABC. A moves towards B with a velocity V, B moves towards C with velocity V, and C moves towards A with same velocity V. Then the velocity of centre of mass of the system of particles is
View Solution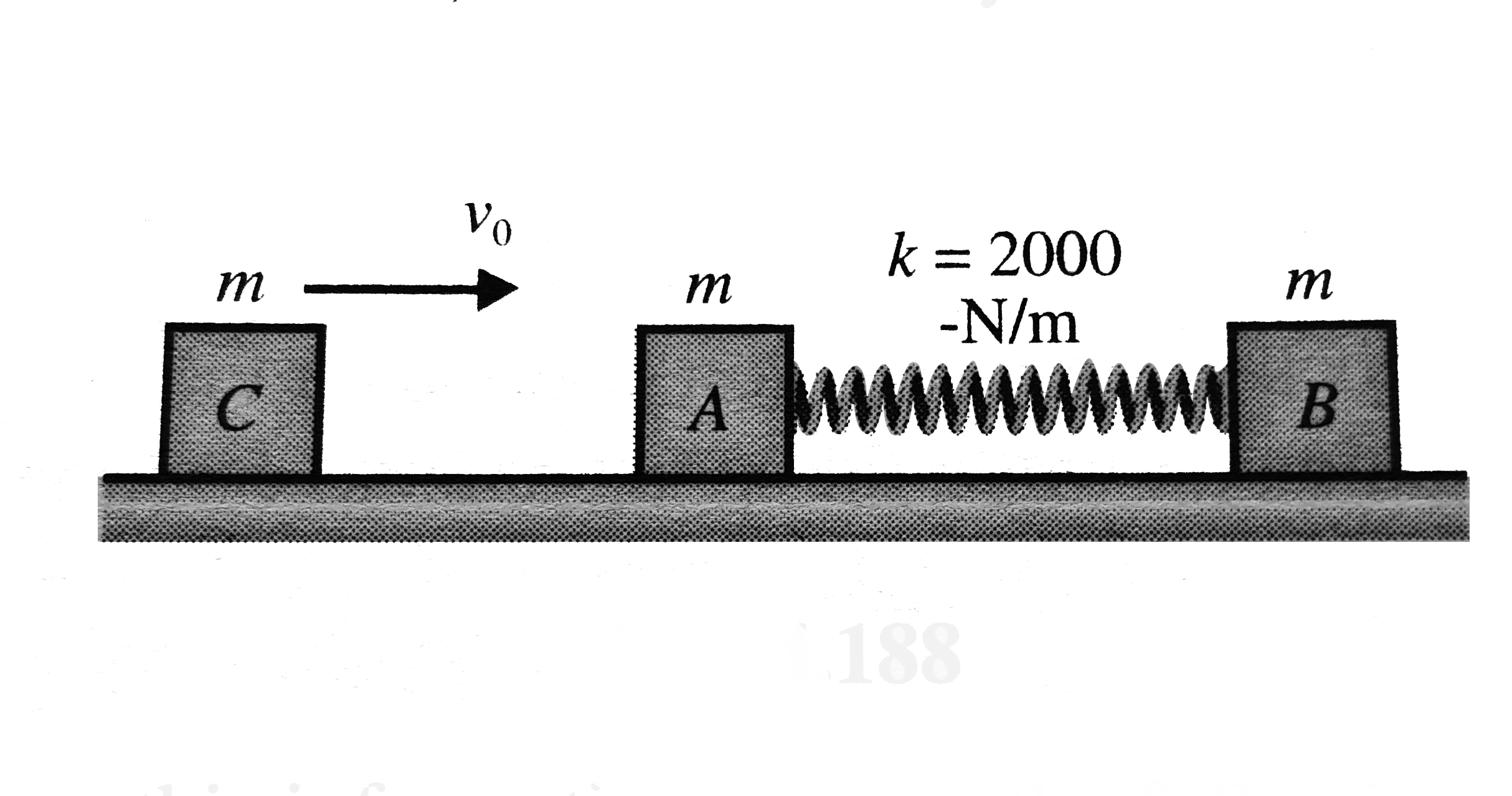
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. After the collision of C and A, the combined body and block B would
Option1
oscillate about centre of mass of system and centre of mass is at rest.
Option2
oscillate about centre of mass of system and centre of mass is moving.
Option3
oscillate but about different location other than the centre of mass.
Option4
not oscillate.
View SolutionThe position Vectors of two identical particles with respect to the origin in the three-dimensional coordinator system are r1andr2 The position of the centre of mass of the system is given by
View SolutionTwo balls of different masses are thrown in air with different velocities. While they are in air acceleration of centre of mass of the system. (neglect air resistance)?
View SolutionAssertion: A constant force F is applied on two blocks and one spring system as shown in figure. Velocity of centre of mass increases linearly with time.

Reason: Acceleration of centre of mass is constant.
View Solution
