A block of mass 2 kg is placed on the floor. The coefficient of static friction it 0.4. A force F of 2.5 N is applied on the block, as shown. calculate the force of friction between the block and the floor. (g=9.8m/s2).
To solve the problem, we need to calculate the force of friction acting between the block and the floor when a force of 2.5 N is applied to the block.
1. Identify the Given Values:
- Mass of the block, m=2kg
- Coefficient of static friction, μ=0.4
- Applied force, F=2.5N
- Acceleration due to gravity, g=9.8m/s2
2. Calculate the Weight of the Block:
The weight W of the block can be calculated using the formula:
W=m⋅g
Substituting the values:
W=2kg⋅9.8m/s2=19.6N
3. Calculate the Maximum Static Friction:
The maximum static friction fmax can be calculated using the formula:
fmax=μ⋅W
Substituting the values:
fmax=0.4⋅19.6N=7.84N
4. Determine the Actual Friction Force:
The actual force of friction f will be the lesser of the applied force F and the maximum static friction fmax. Since the applied force is 2.5 N, we compare it with the maximum static friction:
- Since F=2.5N<fmax=7.84N, the block will not move.
- Therefore, the force of friction f will equal the applied force:
f=F=2.5N
Final Answer:
The force of friction between the block and the floor is 2.5 N.
- Mass of the block, m=2kg
- Coefficient of static friction, μ=0.4
- Applied force, F=2.5N
- Acceleration due to gravity, g=9.8m/s2
The weight W of the block can be calculated using the formula:
W=m⋅g
Substituting the values:
W=2kg⋅9.8m/s2=19.6N
The maximum static friction fmax can be calculated using the formula:
fmax=μ⋅W
Substituting the values:
fmax=0.4⋅19.6N=7.84N
The actual force of friction f will be the lesser of the applied force F and the maximum static friction fmax. Since the applied force is 2.5 N, we compare it with the maximum static friction:
- Since F=2.5N<fmax=7.84N, the block will not move.
- Therefore, the force of friction f will equal the applied force:
f=F=2.5N
The force of friction between the block and the floor is 2.5 N.
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-D
Explore 6 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-B
Explore 13 Videos
- SELF ASSESSMENT PAPER 4Book:ICSEChapter:SELF ASSESSMENT PAPER 4Exercise:Section-D
Explore 6 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM EXPERIMENT TO DETERMINE K
Explore 2 Videos
Similar Questions
A block of mass 2 kg is placed on the floor . The coefficient of static friction is 0.4 . If a force of 2.8 N is applied on the block parallel to floor , the force of friction between the block and floor is : (Taking g = 10m/s2)
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View Solution
Knowledge Check
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 2.5 N is applied on the block as shown in Fig. 15.4.4. The force of friction between the block and the floor is (g=9.8m/s2)
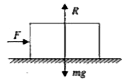 A1.5 NB0.5 NC2.5 NDNone of the above
A1.5 NB0.5 NC2.5 NDNone of the aboveA block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)
 A3 NB8 NC4 ND6 N
A3 NB8 NC4 ND6 N
A block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA crate of mass 100 kg rests on the floor. The coefficient of static friction is 0.4. If a force of 250 N(parallel to the floor) is applied to the create, what's the magnitude of the force of static friction on the crate ?
View SolutionA block is lying static on the floor. The maximum value of static fictional force on the block is 10 N. If a horizontal force of 6 N is applied to the block,what will be the frictional force on the block?
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA block of mass 2 kg is pushed against a rough vertical wall with a force of 40N. Coefficient of static friction being 0.5. Another horizontal force of 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
View SolutionBlock A of mass 3 kg is placed on another block B of mass 5 kg placed on the smooth surface. If coefficient of friction between two blocks is 12 and 32 N force is applied on block B as shown in the figure, then the work done by the frictional force on block A in first two second will be (initial velocity of the system is zero and g=10ms2)
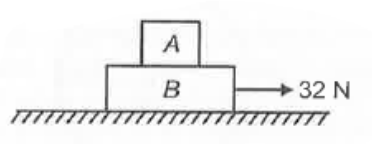
View Solution