What is meant by relative velocity ? Write an expression for the velocity of A and B particle relative to the other moving with velocities v and v along a straight line.
Step by step video & image solution for What is meant by relative velocity ? Write an expression for the velocity of A and B particle relative to the other moving with velocities v_ and v_ along a straight line. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-D6videos
SELF ASSESSMENT PAPER 5
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-B13videos
SELF ASSESSMENT PAPER 5
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 4EXERCISE - Section-D6videos
SELF ASSESSMENT PAPER 4
- BOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM EXPERIMENT TO DETERMINE K2videos
THERMAL CONDUCTION
Similar Questions
Write the expression for Lorentz magnetic force on a particle of charges 'q' moving with velocity →v in a magnetic field →B.
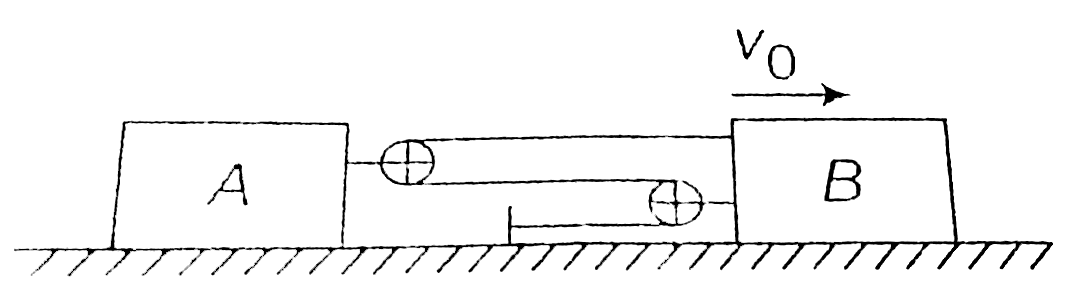
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
View SolutionThe variation of velocity of a particle moving along a straight line is shown in . is
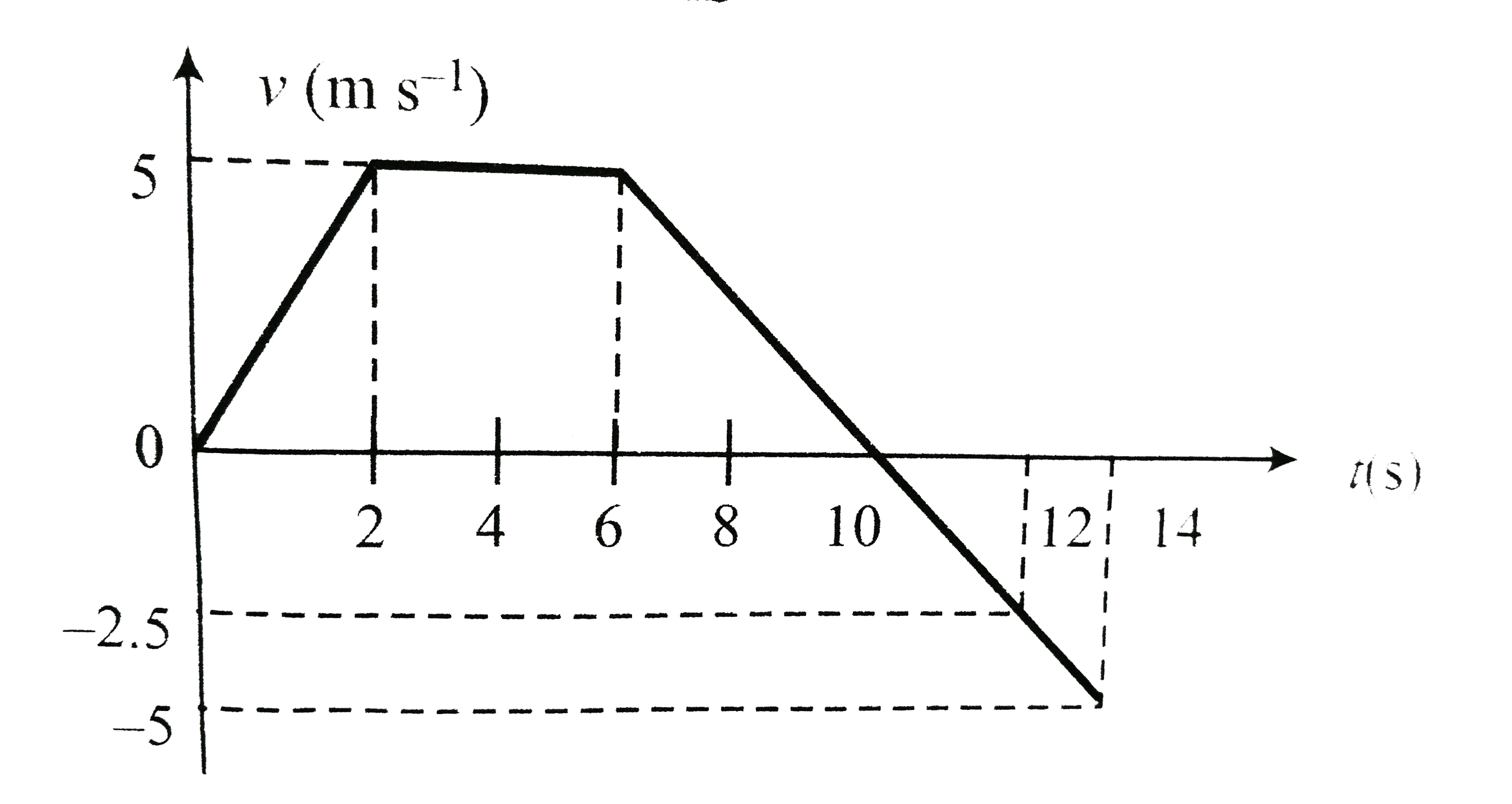.View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is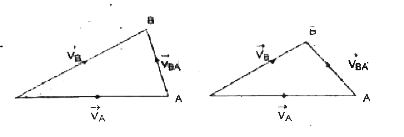
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The velocity of topmost point relative to the bottommost point is
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionStatement-I : If two particles, moving with constant velocities are to meet, the relative velocity must be along the line joining the two particles.
Statement-II : Relative velocity means motion of one particle as viewed from the other.View SolutionThree particles start from the origin at the same time, one with a velocity v1 along the x-axis, second along the y-axis with a velocity v2 and third particle moves along the line x = y. The velocity of third particle, so that three may always lie on the same line is:
View Solution(A) : Relative to an observer at rest in a medium the speed of a mechanical wave in that medium (1) depends only on elastic and other properties (such as mass density) of the medium. It does not depend on the velocity of the source.
(B): For an observer moving with velocity v0 relative to the medium, the speed of a wave is obviously different from v and is given by v±v0View SolutionIn the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.
View Solution