A beam of light converges at a point P. Draw ray diagram to show where the beam will converge if (i) a convex lens and (ii) a concave lens is kept in the path of the beam?
To solve the question, we will draw ray diagrams for both a convex lens and a concave lens to show where a beam of light converges at point P.
Step 1: Draw the Principal Axis
- Begin by drawing a horizontal line across your paper. This line represents the principal axis of the lens.
Step 2: Draw the Convex Lens
- Draw a convex lens shape (which looks like an hourglass) centered on the principal axis. Label the lens as "Convex Lens."
Step 3: Draw the Incoming Rays for the Convex Lens
- Draw three rays coming from the left towards the convex lens:
- The first ray (incident ray) should be parallel to the principal axis.
- The second ray should pass through the center of the lens (undisturbed).
- The third ray should pass through the focus of the lens before reaching the lens.
Step 4: Show the Refraction through the Convex Lens
- For the first ray, after passing through the lens, it will converge at point P on the right side of the lens.
- For the second ray, it continues straight through the lens without bending.
- For the third ray, it will emerge parallel to the principal axis after passing through the lens.
Step 5: Mark the Focus Point
- Mark the point where the rays converge as point P and label it as "Focus."
Step 6: Draw the Concave Lens
- Now, draw a concave lens shape (which looks like a pair of glasses) centered on the principal axis. Label the lens as "Concave Lens."
Step 7: Draw the Incoming Rays for the Concave Lens
- Draw three rays coming from the left towards the concave lens:
- The first ray should be parallel to the principal axis.
- The second ray should pass through the center of the lens (undisturbed).
- The third ray should be directed towards the focus point of the lens.
Step 8: Show the Refraction through the Concave Lens
- For the first ray, after passing through the lens, it will diverge outward as if it were coming from a point on the same side as the incoming rays.
- For the second ray, it continues straight through the lens without bending.
- For the third ray, it will diverge and appear to come from the focus point on the same side of the lens.
Step 9: Mark the Diverging Point
- Mark the point from which the rays appear to diverge as point P and label it as "Virtual Focus."
Final Ray Diagrams:
- You should now have two diagrams: one for the convex lens showing convergence at point P, and another for the concave lens showing divergence with a virtual focus at point P.
- Begin by drawing a horizontal line across your paper. This line represents the principal axis of the lens.
- Draw a convex lens shape (which looks like an hourglass) centered on the principal axis. Label the lens as "Convex Lens."
- Draw three rays coming from the left towards the convex lens:
- The first ray (incident ray) should be parallel to the principal axis.
- The second ray should pass through the center of the lens (undisturbed).
- The third ray should pass through the focus of the lens before reaching the lens.
- For the first ray, after passing through the lens, it will converge at point P on the right side of the lens.
- For the second ray, it continues straight through the lens without bending.
- For the third ray, it will emerge parallel to the principal axis after passing through the lens.
- Mark the point where the rays converge as point P and label it as "Focus."
- Now, draw a concave lens shape (which looks like a pair of glasses) centered on the principal axis. Label the lens as "Concave Lens."
- Draw three rays coming from the left towards the concave lens:
- The first ray should be parallel to the principal axis.
- The second ray should pass through the center of the lens (undisturbed).
- The third ray should be directed towards the focus point of the lens.
- For the first ray, after passing through the lens, it will diverge outward as if it were coming from a point on the same side as the incoming rays.
- For the second ray, it continues straight through the lens without bending.
- For the third ray, it will diverge and appear to come from the focus point on the same side of the lens.
- Mark the point from which the rays appear to diverge as point P and label it as "Virtual Focus."
- You should now have two diagrams: one for the convex lens showing convergence at point P, and another for the concave lens showing divergence with a virtual focus at point P.
Similar Questions
A beam of light converges to a point P.A lens is placed in the path of the convergent beam 12cm from P. At what point does the beam converge if the lens is
(a) a convex lens of focal length 20cm. (b) a concave lens of focal length 16cm ?View SolutionA beam of light converges at a point P. Now a convex lens is placed in the part of the converngent beam at 15 cm from P. At what point does a beam converge if the convex lens has a focad length 10 cm ?
View SolutionA beam of light converges to a point P. A lens is placed in the path of the covergent beam 12cm from P. At what point does the beam converge if the lens is
(a) a convex lens of focal length 20cm
(b) a concave lens of focal length 16cm ?View SolutionDraw a ray diagram to show how a convex lens can be used as a magnifying glass.
View SolutionA beam of light is converging towards a point. A plane parallel plate of glass of thickness t, refractive index μ is introduced in the path of the beam. The convergent point is shifted by (assume near normal incidence) :
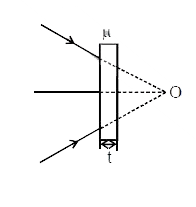 View Solution
View SolutionA beam of light converges to a point on a screen S. A mirror is placed in front of the screen at a distance of 10cm form the screen. It is found that the beam now converges at a point 20cm in front of the mirror. Find the focal length of the mirror.
View SolutionA converging beam of light is incident on a concave lens of focal length 20 cm. In the absence of the lens, the beam converges at a point 10 m behind the lens. Find where the beam will converge/diverge after refraction.
View SolutionFigure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
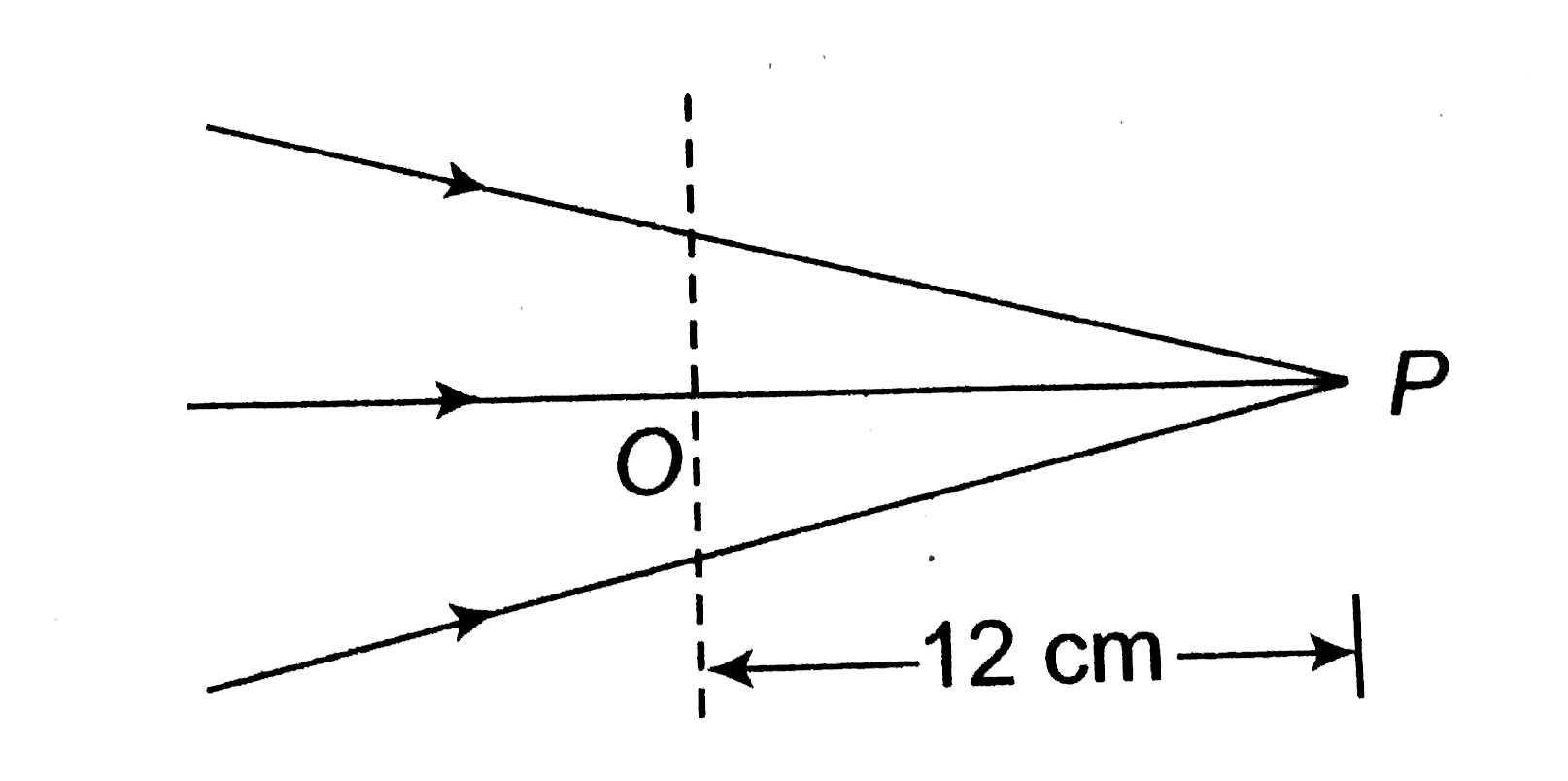 View Solution
View SolutionThe rays of different colours fail to converge at a point after going through a converging lens. This defect is called
View SolutionA beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Similarly, as in above question when point O is 30cm behind the mirror.View Solution

