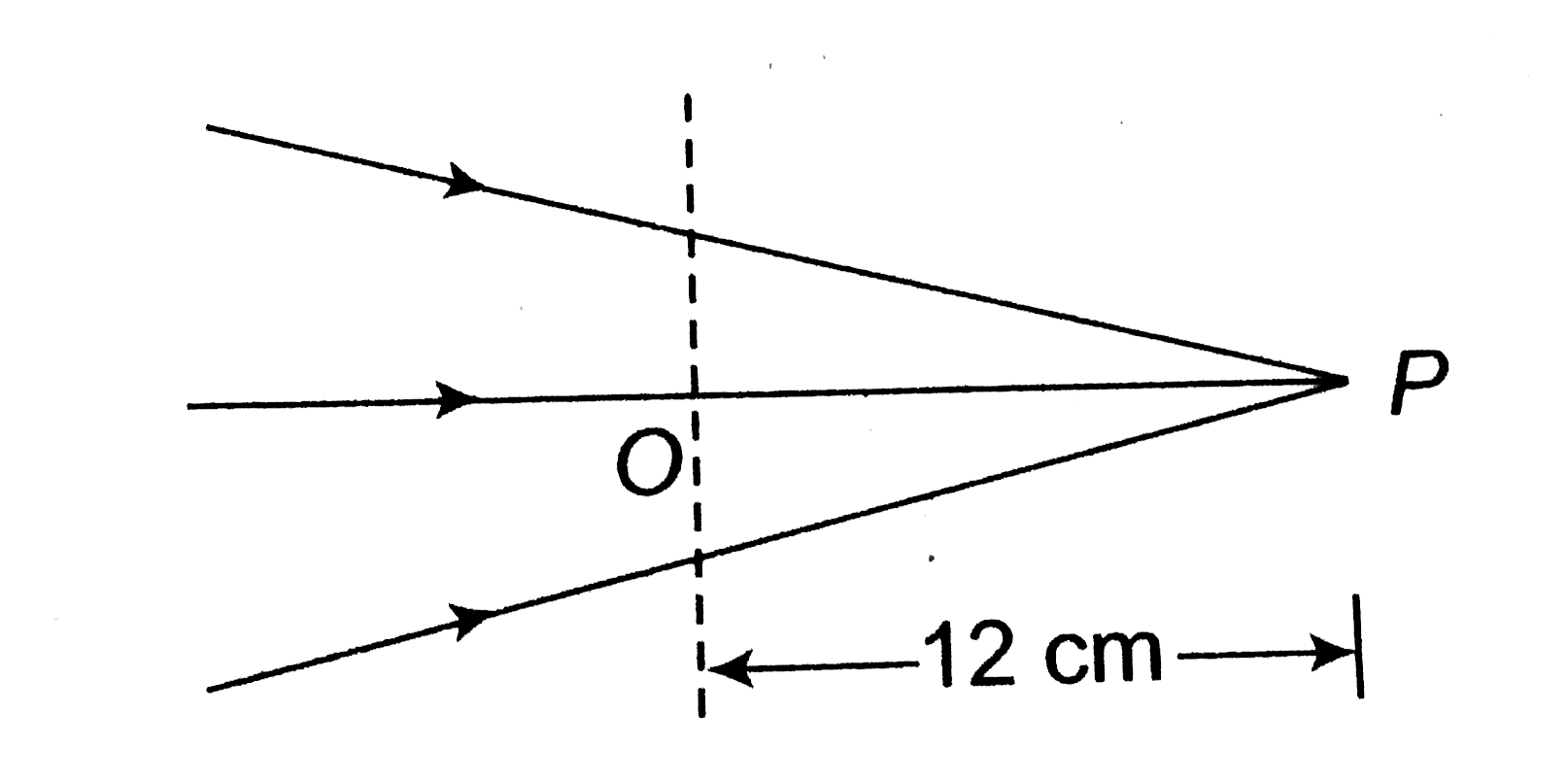
A beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Similarly, as in above question when point O is 30cm behind the mirror.
2(virtual, inverted)
3(real, inverted)
3(virtual, enlarged)
1(real, enlarged)
The correct Answer is:a.
To solve the problem step by step, we will follow the concepts of geometrical optics, specifically focusing on the convex mirror and its properties.
Step 1: Identify the Given Values
- Focal length of the convex mirror (f) = +20 cm (positive because it is a convex mirror)
- Distance of the object (u) = -30 cm (negative because the object is behind the mirror)
Step 2: Use the Mirror Formula
The mirror formula is given by:
1f=1v+1u
Where:
- f = focal length
- v = image distance
- u = object distance
Step 3: Substitute the Values into the Mirror Formula
Substituting the values of f and u into the mirror formula:
120=1v+1−30
Step 4: Rearrange the Equation
Rearranging the equation gives:
1v=120+130
Step 5: Find a Common Denominator
The common denominator for 20 and 30 is 60. Thus, we can rewrite the fractions:
120=360,130=260
So,
1v=360+260=560
Step 6: Calculate the Image Distance (v)
Now, taking the reciprocal to find v:
v=605=12 cm
(Note: The positive sign indicates that the image is virtual and located behind the mirror.)
Step 7: Calculate the Magnification (M)
The magnification (M) is given by the formula:
M=−vu
Substituting the values of v and u:
M=−12−30=1230=25
Step 8: Interpret the Results
The magnification of 25 means that the image is virtual, upright, and smaller than the object.
Final Results
- Image distance (v) = 12 cm (behind the mirror)
- Magnification (M) = 25
- Focal length of the convex mirror (f) = +20 cm (positive because it is a convex mirror)
- Distance of the object (u) = -30 cm (negative because the object is behind the mirror)
The mirror formula is given by:
1f=1v+1u
Where:
- f = focal length
- v = image distance
- u = object distance
Substituting the values of f and u into the mirror formula:
120=1v+1−30
Rearranging the equation gives:
1v=120+130
The common denominator for 20 and 30 is 60. Thus, we can rewrite the fractions:
120=360,130=260
So,
1v=360+260=560
Now, taking the reciprocal to find v:
v=605=12 cm
(Note: The positive sign indicates that the image is virtual and located behind the mirror.)
The magnification (M) is given by the formula:
M=−vu
Substituting the values of v and u:
M=−12−30=1230=25
The magnification of 25 means that the image is virtual, upright, and smaller than the object.
- Image distance (v) = 12 cm (behind the mirror)
- Magnification (M) = 25
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives
7 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Find the magnification and nature of the image when point O is 10cm behind the mirror.
View SolutionFor a concave mirror of focal length 20 cm, match the following

View SolutionFrom a concave mirror of focal length 20 cm. match the following:

View SolutionAn object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by a mirror is
View SolutionThe image formed by a convex mirror of focal length 30cm. is a quarter of the object. What is the distance of the object from the mirror ?
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
View SolutionA concave mirror of focal length 10cm and a convex mirror of focal length 15cm are placed facing each other 40cm apart. A point object is placed between the mirrors, on their common axis and 15cm from the concave mirror. Find the position and nature of the image produced by successive reflections, first at the concave mirror and then at the convex mirror.
View SolutionFocal length of a convex mirror is 10 cm
View SolutionAn object is placed at a distance 20 cm from the pole of a convex mirror of focal length 20 cm. The image is produced at
View SolutionFigure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
View Solution
