What is the amount of work done in moving a point charge around a circular are of radius r at the centre where another point charge is located ?
To find the amount of work done in moving a point charge around a circular arc of radius r at the center where another point charge is located, we can follow these steps:
1. Identify the Charges: Let Q be the charge located at the center of the circular arc and q be the charge that we are moving along the arc.
2. Understand the Electric Field: The electric field E due to the charge Q at a distance r from it is given by the formula:
E=kQr2
where k is Coulomb's constant.
3. Direction of the Electric Field: The electric field due to charge Q will radiate outward from Q. When moving the charge q along the circular arc, the direction of the electric field is always perpendicular to the tangent of the circular path at any point.
4. Work Done Formula: The work done W in moving a charge in an electric field is given by:
W=F⋅d=F⋅d⋅cosθ
where F is the force on charge q, d is the displacement, and θ is the angle between the force and the displacement.
5. Angle Between Force and Displacement: As we move the charge q along the circular arc, the angle θ between the force (which is in the direction of the electric field) and the displacement (which is tangential to the arc) is always 90∘.
6. Cosine of 90 Degrees: Since cos90∘=0, we can substitute this into the work done formula:
W=F⋅d⋅cos(90∘)=F⋅d⋅0=0
7. Conclusion: Therefore, the total work done in moving the charge q around the circular arc is:
W=0
Final Answer:
The amount of work done in moving the point charge around the circular arc is 0.
E=kQr2
where k is Coulomb's constant.
W=F⋅d=F⋅d⋅cosθ
where F is the force on charge q, d is the displacement, and θ is the angle between the force and the displacement.
W=F⋅d⋅cos(90∘)=F⋅d⋅0=0
W=0
The amount of work done in moving the point charge around the circular arc is 0.
Similar Questions
Knowledge Check
The work done in carrying a charge q once round a circle of radius r with a charge Q at the centre is
AqQ4πε0aBqQ4πε0a2Cq4πε0aDzeroA charge is distributed with a linear density λ over a rod of the length L placed along radius vector drawn from the point where a point charge q is located. The distance between q and the nearest point on linear charge is R. The electrical force experienced by the linear charge due to q is
AqλL4πε0R2BqλL4πε0R(R+L)CqλL4πε0RLDqλL4πε0L2In figure below a charge Q is fixed. Another charge q is moved along a circular arc MN of radius r around it, from the point M to the point N such that the length of the arc MN = 1. The work done in this process is :
 AZeroBI4πε0⋅Qqr2lCQq2ε0r2lDQq2πε0r2
AZeroBI4πε0⋅Qqr2lCQq2ε0r2lDQq2πε0r2
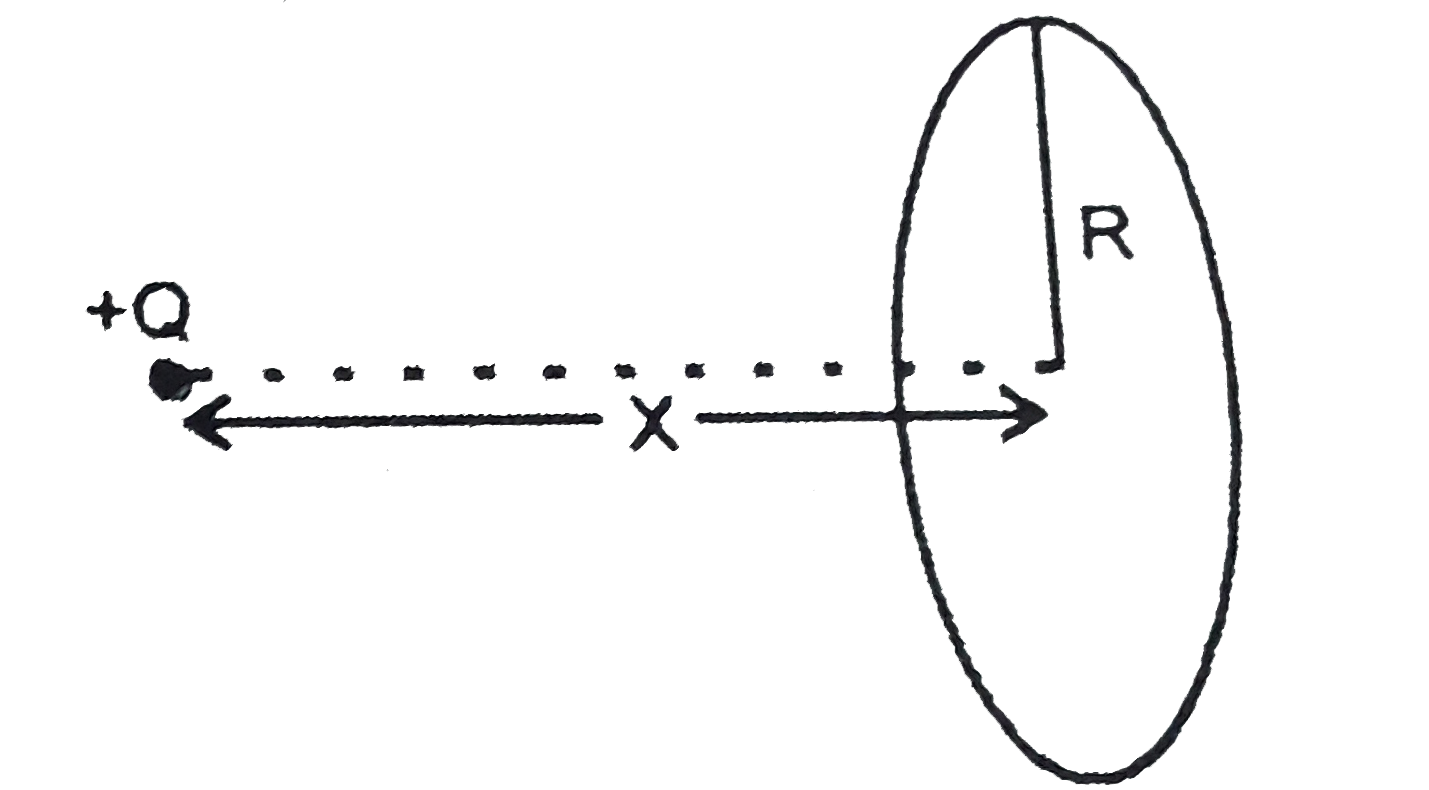
Find the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
View SolutionThe work done in carrying a point charge form one point to another in an electrostatic field depends on the path along which the point charge is carried.
View SolutionWhen an electron moves in a circular path around a stationary nucleus charge at the center
View SolutionThe are AB with the centre C and infinitely long wire having linear charge density λ are lying in the same plane. The minium amount of work to be done to move a point charge q0 from point A to B through a circular path AB of radius a is equal to
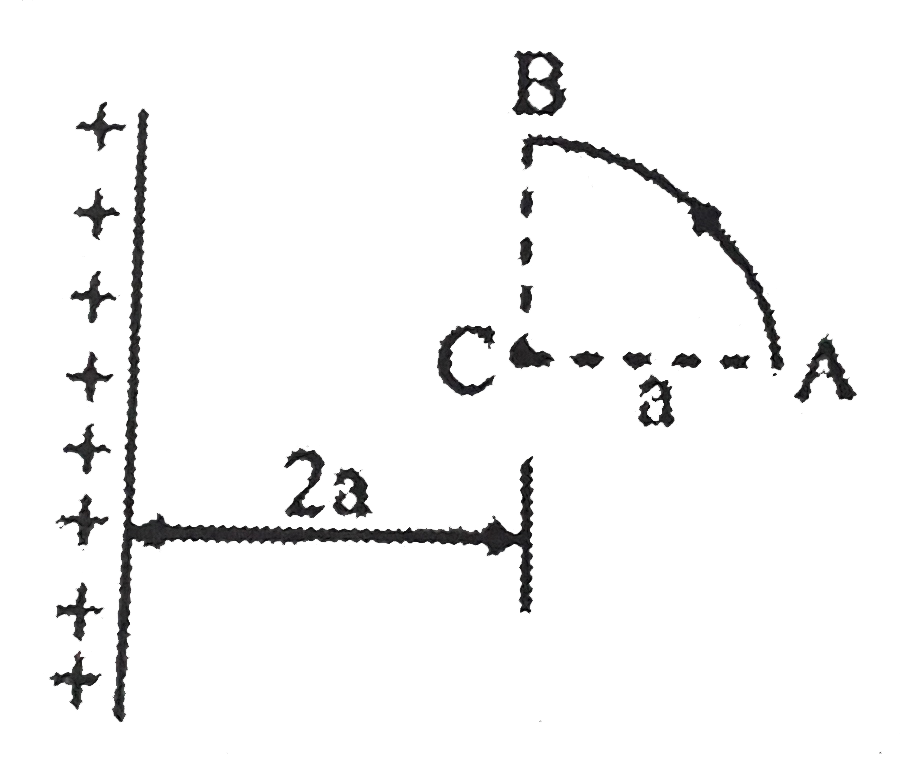
View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:

View Solution
