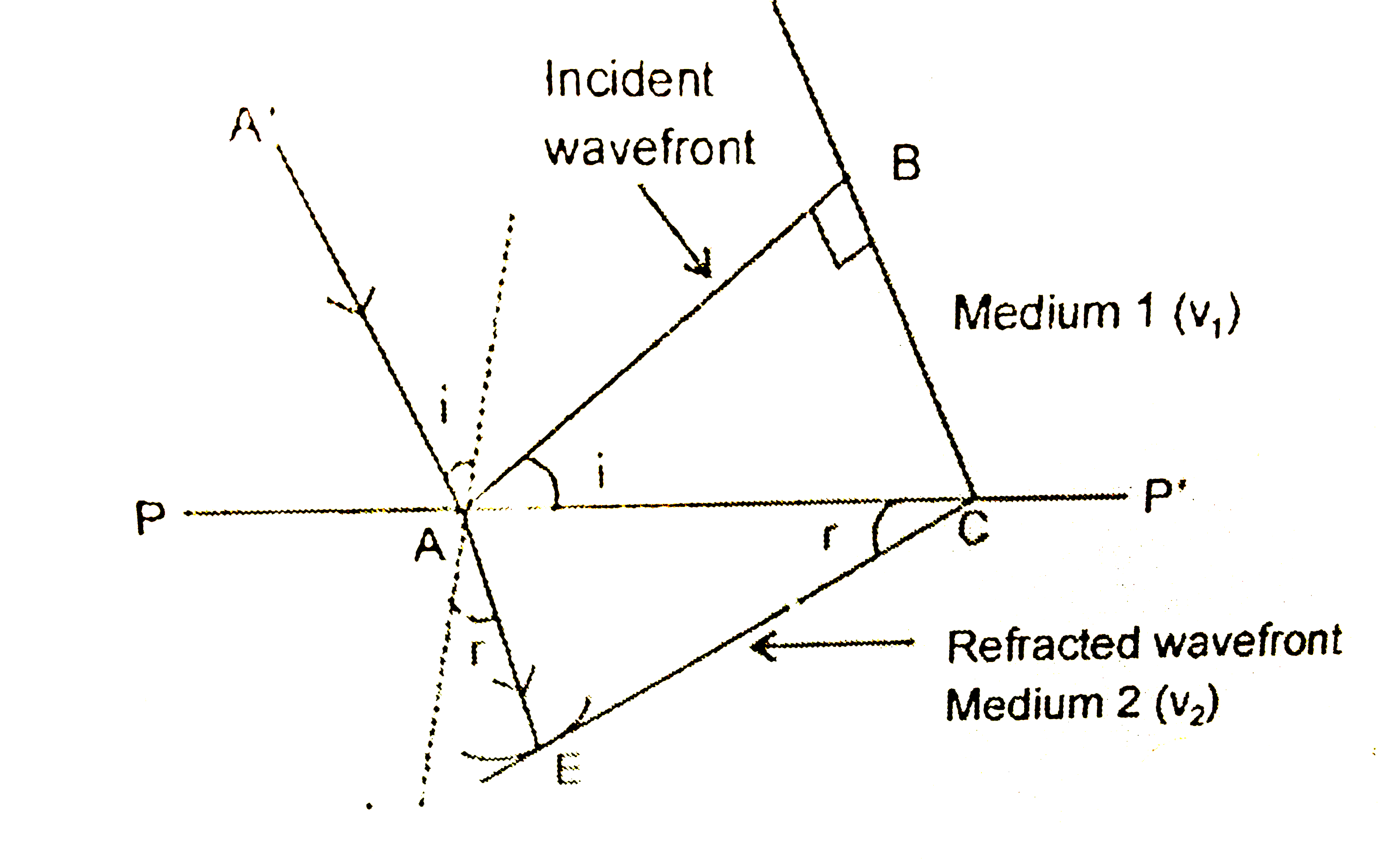
Use Huygen's principle to show how a plane wavefront propagates from a denser to rarer medium. Hence, verify snell's law of refraction.
Consider a plane surface XY separating a denser medium of refractive index from a rarer medium of refractive index . Let be the values of speed of light in the two media, where . AB is a plane wavefront incident on XY at an angle . Let at a given instant the end A of the wavefront just strikes the surface XY but the other end B has still to cover a path BC. if it takes time , then .
Meanwhile, point A begins to emit secondary wavelets which cover a distance in second medium in time t. draw a circular arc with a as centre and as radius and draw a tangent CD from point C o this arc. then CD is the refracted wavefront in the rarer medium which advances in the direction of rays 1.2.. the refracted wavefront subtends an angle r from surface XY.
Now in

and in
a constant.
Which is snell.s law of refractive.
Topper's Solved these Questions
- WAVE OPTICSBook:U-LIKE SERIESChapter:WAVE OPTICSExercise:LONG ANSWER QUESTIONS-II
Explore 12 Videos
- WAVE OPTICSBook:U-LIKE SERIESChapter:WAVE OPTICSExercise:SELF ASSESSMENT TEST SECTION A (MULTIPLE CHOICE QUESTIONS)
Explore 6 Videos
- WAVE OPTICSBook:U-LIKE SERIESChapter:WAVE OPTICSExercise:SHORT ANSWER QUESTIONS
Explore 29 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:U-LIKE SERIESChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:SECTION B
Explore 1 Video
Similar Questions
Knowledge Check
According to Huygens' principle, a wavefront propagates through a medium by
Apushing medium particlesBpropagating through medium with speed of lightCcarrying particles of same phase along with itDcreating secondary wavelets which forms a new wavefront
(a) State Huygen's principle . Using this principle draw a diagram to show how a plane wave front incident at the interface of the media gets refracted when it propagates from a rarer to a denser medium. Hence verify Snell's law of refraction.
(b) When monochromatic light travels from a rarer to a denser medium, explain the following, giving reasons-
(i) Is the frequency of reflected and refracted light same as the frequency of incident light?
(ii) Does the decrease in speed imply a reduction in the energy carried by light wave?
View SolutionHow is a wavefront defined? Using Huygen's construction , draw a figure showing the propagation of a plane wave refracting at a plane surface separating two media. Hence verify Snell's law of refraction.
View SolutionHow is a wavefront defined ? Using Hygen's construction draw a figure showing the propagation of a plane wave refracting at a plane surface separating two media. Hence verify Snell'a law of refraction.
View SolutionUsing Huygen.s principle, verify Snell.s law of refraction of plane wave propagating from denser medium to rarer medium.
View SolutionWhat is a wavefront? How does it propagate? Using Huygens' principle, explain reflection of a plane wavefront from a surface and verify the laws of reflection.
View SolutionDefine the term wavefront. Using Huygens' wave theory, verify the laws of reflection.
View SolutionA plane wavefront propagating from a rarer into a denser medium is incident at an angle of incidence i on a refracting surface. Draw a diagram showing incident wavefront and refracted wavefront . Hence verify Snell's laws of refraction.
View Solution