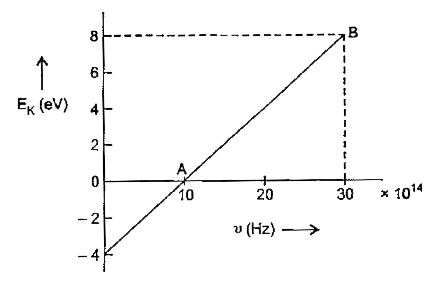
In an experiment of photoelectric effect, the graph of maximum kinetic energy $E_{K}$ of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in Figure below:
Find : (i) Threshold frequency of the metal.
(ii) work function of the metal
(iii) Stopping potential for the photoelectrons emitted by the light of frequency $v = 30 \times 10^{14}$ Hz.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the question regarding the photoelectric effect, we will follow these steps:
Step 1: Determine the Threshold Frequency
The threshold frequency ( $v_{0}$ ) is the frequency at which the maximum kinetic energy ( $E_{K}$ ) of the emitted photoelectrons becomes zero. From the graph, this corresponds to the x-intercept of the line AB.
From the graph:
- The x-intercept occurs at $v = 10 \times 10^{14} Hz$ .
Answer:
(i) The threshold frequency of the metal is $v_{0} = 10 \times 10^{14} Hz$ .
Step 2: Calculate the Work Function
The work function ( $W$ ) of the metal can be calculated using the formula:
$W = h \cdot v_{0}$
where $h$ is Planck's constant ( $6.626 \times 10^{- 34} J s$ ).
Calculation:
- Convert the threshold frequency to Joules:
$W = (6.626 \times 10^{- 34} J s) \cdot (10 \times 10^{14} Hz) = 6.626 \times 10^{- 20} J$
- Convert Joules to electronvolts (1 eV = $1.6 \times 10^{- 19} J$ ):
$W = \frac{6.626 \times 10^{- 20} J}{1.6 \times 10^{- 19} J/eV} \approx 0.414 eV$
Answer:
(ii) The work function of the metal is $W \approx 0.414 eV$ .
Step 3: Calculate the Stopping Potential
The stopping potential ( $V_{s}$ ) can be calculated using the formula:
$e V_{s} = E_{K}$
where $E_{K}$ is the maximum kinetic energy of the emitted photoelectrons when the frequency $v = 30 \times 10^{14} Hz$ .
Calculation of Maximum Kinetic Energy:
Using the equation for kinetic energy:
$E_{K} = h (v - v_{0})$
Substituting the values:
$E_{K} = h (30 \times 10^{14} - 10 \times 10^{14}) = h (20 \times 10^{14})$
$E_{K} = (6.626 \times 10^{- 34}) \cdot (20 \times 10^{14}) = 1.3252 \times 10^{- 19} J$
Convert to eV:
$E_{K} = \frac{1.3252 \times 10^{- 19}}{1.6 \times 10^{- 19}} \approx 0.828 eV$
Stopping Potential Calculation:
The stopping potential is given by:
$V_{s} = \frac{E_{K}}{e}$
Thus:
$V_{s} \approx 0.828 volts$
Answer:
(iii) The stopping potential for the photoelectrons emitted by the light of frequency $v = 30 \times 10^{14} Hz$ is approximately $V_{s} \approx 0.828 volts$ .
Summary of Answers:
(i) Threshold frequency $v_{0} = 10 \times 10^{14} Hz$
(ii) Work function $W \approx 0.414 eV$
(iii) Stopping potential $V_{s} \approx 0.828 volts$

Updated on:7/8/2024

According to Einstein's photoelectric equation, the plot of the maximum kinetic energy of the emitted photoelectrons from a metal versus frequency of the incident radiation gives a straight line whose slope
Adepends on the intensity of incident radiation.
Bdepends on the nature of the metal and also on the intensity of incident radiation.
Cis same for all metals and independent of the intensity of the incident radiation.
Ddepends on the nature of the metal.