Obtain an expression for refraction at a single convex spherical surface separating the two media having refractive indices μ1(rarer medium) and μ2(denser medium) i.e., a relation between u,v,μ1,μ2 and R.
To derive the expression for refraction at a single convex spherical surface separating two media with refractive indices μ1 (for the rarer medium) and μ2 (for the denser medium), we will follow these steps:
Step 1: Diagram and Definitions
- Draw a convex spherical surface separating two media.
- Let the object be located in the rarer medium (with refractive index μ1) and the image be formed in the denser medium (with refractive index μ2).
- Define the following points:
- P: The pole of the spherical surface.
- C: The center of curvature.
- O: The object point.
- I: The image point.
- R: The radius of curvature of the convex surface.
Step 2: Apply Snell's Law
Using Snell's Law at the point of incidence, we have:
μ1sini=μ2sinr
where i is the angle of incidence and r is the angle of refraction.
Step 3: Geometry of the Refraction
From the geometry of the situation, we can relate the angles:
- Let α be the angle of incidence, β be the angle of refraction, and γ be the angle between the normal and the line joining the center of curvature to the point of incidence.
Using the exterior angle property of triangles:
i=α+β
and from the triangle formed at the point of incidence:
r=β−γ
Step 4: Small Angle Approximation
For small angles, we can use the approximation:
sinθ≈tanθ≈θ
Thus, we can write:
μ1α+μ1β=μ2(β−γ)
Step 5: Rearranging the Equation
Rearranging the equation gives:
μ1α+μ2γ=μ2β−μ1β
This simplifies to:
μ1α+μ2γ=(μ2−μ1)β
Step 6: Relating Angles to Distances
Using the definitions of tangent in terms of distances:
- tanα=QP′OP′
- tanγ=QP′IP′
- tanβ=QP′CP′
Substituting these into the equation gives:
μ1QP′OP′+μ2QP′IP′=(μ2−μ1)QP′CP′
Step 7: Canceling Common Terms
Since QP′ is common in all terms, it cancels out:
μ11OP′+μ21IP′=(μ2−μ1)1CP′
Step 8: Substituting Distances
Let:
- OP′=−u (object distance)
- IP′=v (image distance)
- CP′=R (radius of curvature)
Substituting these into the equation gives:
μ11−u+μ21v=μ2−μ1R
Step 9: Final Expression
Rearranging the equation leads to:
μ2v−μ1u=μ2−μ1R
This is the required expression for refraction at a single convex spherical surface.
- Draw a convex spherical surface separating two media.
- Let the object be located in the rarer medium (with refractive index μ1) and the image be formed in the denser medium (with refractive index μ2).
- Define the following points:
- P: The pole of the spherical surface.
- C: The center of curvature.
- O: The object point.
- I: The image point.
- R: The radius of curvature of the convex surface.
Using Snell's Law at the point of incidence, we have:
μ1sini=μ2sinr
where i is the angle of incidence and r is the angle of refraction.
From the geometry of the situation, we can relate the angles:
- Let α be the angle of incidence, β be the angle of refraction, and γ be the angle between the normal and the line joining the center of curvature to the point of incidence.
i=α+β
and from the triangle formed at the point of incidence:
r=β−γ
For small angles, we can use the approximation:
sinθ≈tanθ≈θ
Thus, we can write:
μ1α+μ1β=μ2(β−γ)
Rearranging the equation gives:
μ1α+μ2γ=μ2β−μ1β
This simplifies to:
μ1α+μ2γ=(μ2−μ1)β
Using the definitions of tangent in terms of distances:
- tanα=QP′OP′
- tanγ=QP′IP′
- tanβ=QP′CP′
μ1QP′OP′+μ2QP′IP′=(μ2−μ1)QP′CP′
Since QP′ is common in all terms, it cancels out:
μ11OP′+μ21IP′=(μ2−μ1)1CP′
Let:
- OP′=−u (object distance)
- IP′=v (image distance)
- CP′=R (radius of curvature)
μ11−u+μ21v=μ2−μ1R
Rearranging the equation leads to:
μ2v−μ1u=μ2−μ1R
Similar Questions
Derive an expression for refraction at a single (convex) spherical surface, i.e., a relation between u, v, R, n1 (rarer medium) and n2 (denser medium), where the terms have their usual meaning.
View SolutionIf a ray of light is incident from rarer medium at an angle 45° on the surface which separates two medium having refractive indices 1 and √2 for rarer and denser medium, then angle of deviation of refractive ray with incident ray is
View SolutionThere are three optical media 1,2 and 3 with the refractive indices μ1>μ2>μ3.
(TIR → total internal reflection)View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
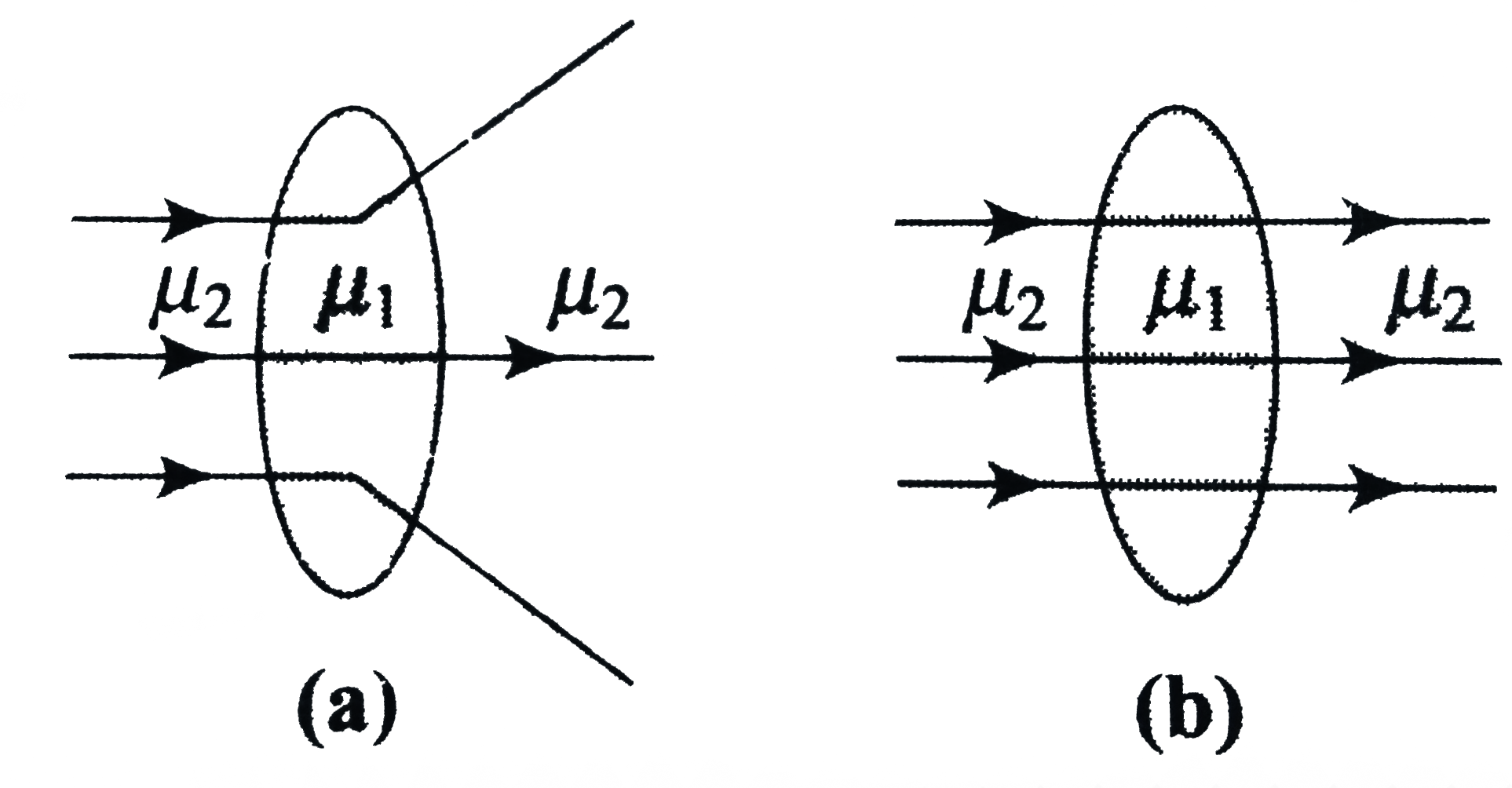 View Solution
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
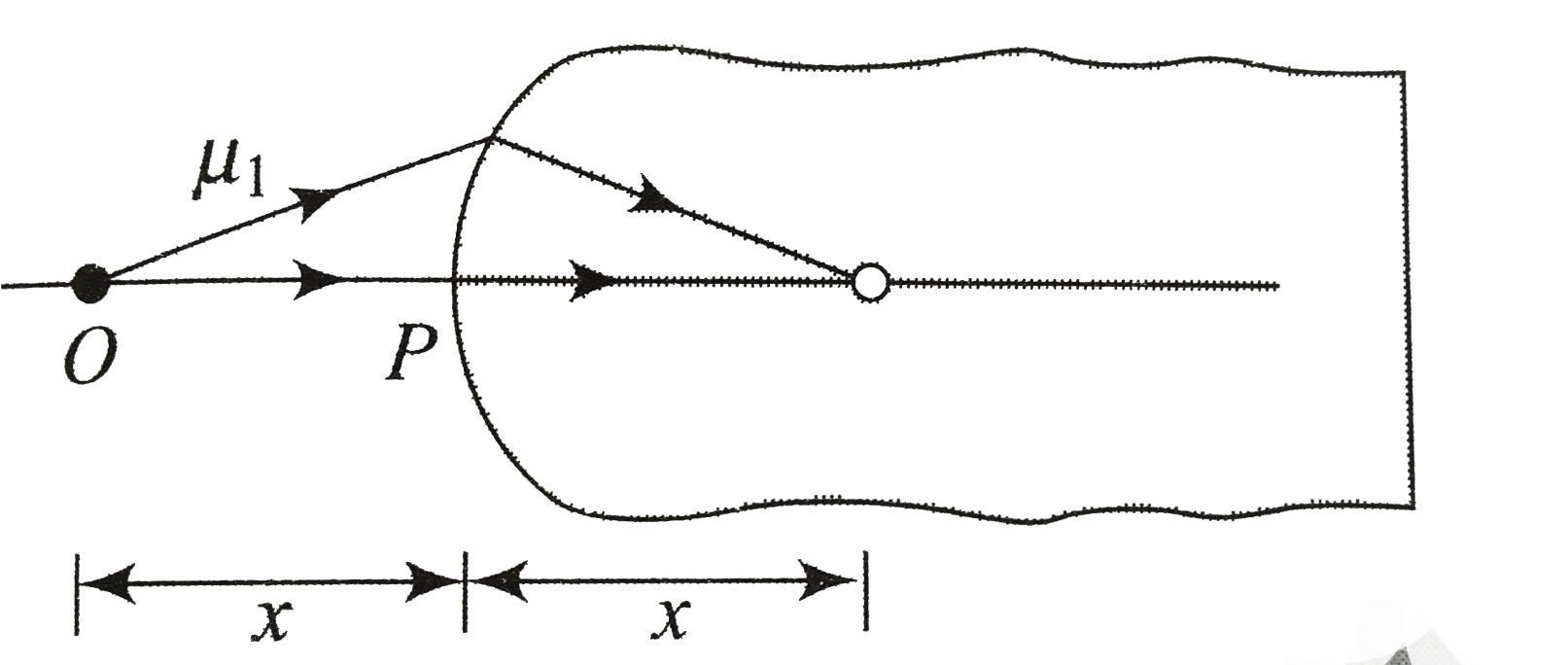 View Solution
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
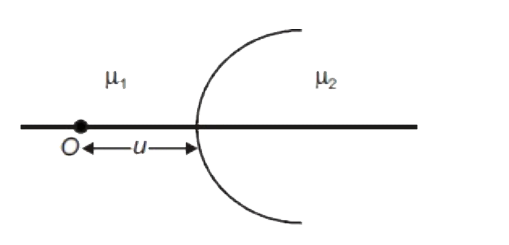 View Solution
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
View SolutionIf a convex lens of refractive index μl is placed in a medium of refractive index μm Such that μl>μm>μair then
View SolutionRefraction takes place at a convex spherical boundary separating air-glass medium. For the image to be real, the object distance (μg=3/2)
Note Object lying in the glass.View Solution

