By splitting the figure given alongside into rectangles, find the area.
The correct Answer is:9
To find the area of the given figure by splitting it into rectangles, we can follow these steps:
1. Identify the Dimensions of the Figure:
- The figure can be split into three rectangles.
- Let's denote the rectangles as A (ABIJ), B (CDHI), and C (EFGH).
- From the problem, we know that the height of each rectangle is 1 unit.
2. Determine the Lengths of Each Rectangle:
- For rectangle A (ABIJ), the length is 3 units.
- For rectangle B (CDHI), the length is also 3 units.
- For rectangle C (EFGH), the length is again 3 units.
3. Calculate the Area of Each Rectangle:
- The area of rectangle A (ABIJ) = Length × Height = 3 × 1 = 3 square units.
- The area of rectangle B (CDHI) = Length × Height = 3 × 1 = 3 square units.
- The area of rectangle C (EFGH) = Length × Height = 3 × 1 = 3 square units.
4. Sum the Areas of All Rectangles:
- Total area = Area of A + Area of B + Area of C
- Total area = 3 + 3 + 3 = 9 square units.
Final Answer:
The total area of the figure is 9 square units.
- The figure can be split into three rectangles.
- Let's denote the rectangles as A (ABIJ), B (CDHI), and C (EFGH).
- From the problem, we know that the height of each rectangle is 1 unit.
- For rectangle A (ABIJ), the length is 3 units.
- For rectangle B (CDHI), the length is also 3 units.
- For rectangle C (EFGH), the length is again 3 units.
- The area of rectangle A (ABIJ) = Length × Height = 3 × 1 = 3 square units.
- The area of rectangle B (CDHI) = Length × Height = 3 × 1 = 3 square units.
- The area of rectangle C (EFGH) = Length × Height = 3 × 1 = 3 square units.
- Total area = Area of A + Area of B + Area of C
- Total area = 3 + 3 + 3 = 9 square units.
The total area of the figure is 9 square units.
Similar Questions
By splitting the following figures into rectangles, find their areas(The measures are given in centimetres).
View SolutionIn the figure given alongside.
Name the adjacent angles.
View SolutionSplit the following shapes into rectangles and find their areas. (The measures are given in centimetres)
View SolutionThe shaded portion of the figure, given alongside, shows two concentric circles.
If the circumference of the two circles be 396 cm and 374 cm, find the area of the shaded portion.

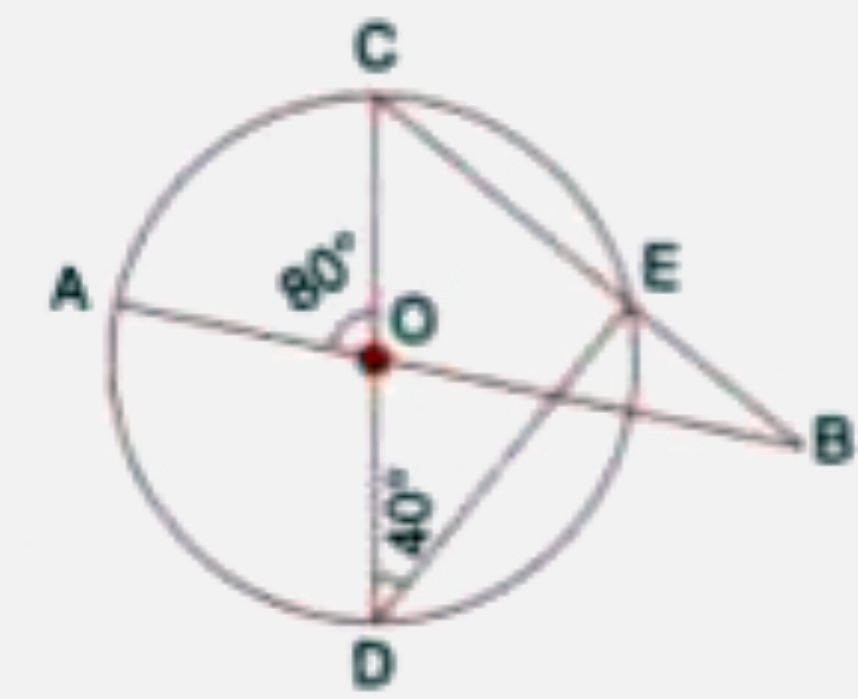
View SolutionIn the figure given alongside ,AB and CD are straight lines thorugh the centre O of a circle. If ∠AOC=80∘and∠CDE=40∘ , find ∠DCE
View SolutionFind what per cent of the figure given alongside is shaded and what per cent is not shaded.

View SolutionIn the figure, given alongside, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and area of ΔPOB−120cm2. find the area of ΔQOA.

View SolutionIn the figure, given alongside, CD is a diameter which meets the chord AB at E, such that AE = BE = 4 cm. If CE is 3 cm, find the radius of the circle.
View SolutionIn the figure given alongside, mark compressions and rarefactions of a wave as the tuning fork is vibrating. Also mark one complete wave.

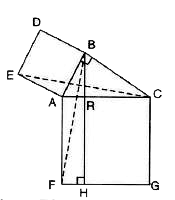
View SolutionIn the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH perpendicular to FG, prove that :
(i) ΔEAC≅ΔBAF.
(ii) Area of the square ABDE
= Area of the rectangle ARHF.
View Solution
