In the figure, given alongside, CD is a diameter which meets the chord AB at E, such that AE = BE = 4 cm. If CE is 3 cm, find the radius of the circle.
The correct Answer is:416 cm
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Identify Given Information:
- AE = BE = 4 cm (since E is the midpoint of AB)
- CE = 3 cm
- CD is the diameter of the circle.
2. Define Variables:
- Let the radius of the circle be r.
- Since O is the center of the circle, we have OA=r and OC=r.
3. Use the Property of Chords:
- Since OE is perpendicular to chord AB at point E (because OE bisects AB), we can use the Pythagorean theorem in triangle OAE.
4. Find OE:
- We know that OE=OC−CE.
- Therefore, OE=r−3 (since CE = 3 cm).
5. Apply the Pythagorean Theorem:
- In triangle OAE, we have:
OA2=OE2+AE2
- Substituting the known values:
r2=(r−3)2+42
6. Expand and Simplify:
- Expanding (r−3)2:
r2=(r2−6r+9)+16
- Simplifying the equation:
r2=r2−6r+25
- Canceling r2 from both sides:
0=−6r+25
- Rearranging gives:
6r=25
- Therefore:
r=256 cm
7. Convert to Mixed Fraction or Decimal:
- Converting 256 to a mixed fraction:
25÷6=4 remainder 1⇒416 cm
- As a decimal:
r≈4.16 cm
Final Answer:
The radius of the circle is 256 cm or approximately 4.16 cm.
---
- AE = BE = 4 cm (since E is the midpoint of AB)
- CE = 3 cm
- CD is the diameter of the circle.
- Let the radius of the circle be r.
- Since O is the center of the circle, we have OA=r and OC=r.
- Since OE is perpendicular to chord AB at point E (because OE bisects AB), we can use the Pythagorean theorem in triangle OAE.
- We know that OE=OC−CE.
- Therefore, OE=r−3 (since CE = 3 cm).
- In triangle OAE, we have:
OA2=OE2+AE2
- Substituting the known values:
r2=(r−3)2+42
- Expanding (r−3)2:
r2=(r2−6r+9)+16
- Simplifying the equation:
r2=r2−6r+25
- Canceling r2 from both sides:
0=−6r+25
- Rearranging gives:
6r=25
- Therefore:
r=256 cm
- Converting 256 to a mixed fraction:
25÷6=4 remainder 1⇒416 cm
- As a decimal:
r≈4.16 cm
The radius of the circle is 256 cm or approximately 4.16 cm.
Topper's Solved these Questions
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(A)
14 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)
15 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
Similar Questions
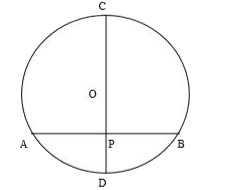
In the figure given below, CD is the diameter of the circle which meets the chord AB at P such that AP = BP = 12 cm. If DP = 8 cm, find the radius of the circle.
View SolutionIn the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If AC=8cm, BE=2cm, then find the radius of the circle.

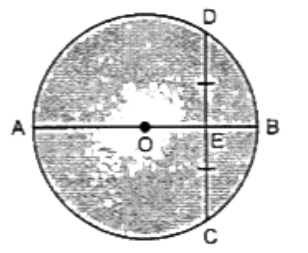
View SolutionThe figure, given below, show a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm. Find the radius of the circle.
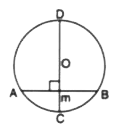
View SolutionIn the given figure, the diameter CD of a circle with centre 0 is perpendicular to the chord AB.
If AB = 8 cm and CM = 2 cm, find the radius of the circle.
View SolutionIn the given figure, OP=13 cm, AB=7 cm and BP=9 cm. Find the radius of the circle.

View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionThe shaded portion of the figure, given alongside, shows two concentric circles.
If the circumference of the two circles be 396 cm and 374 cm, find the area of the shaded portion.

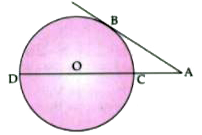
View SolutionIn the given figure O is the centre of the circle and AB is a tangents at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle on opposite sides of a diameter such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords.
View SolutionAD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
View Solution
