If the angle of incidence is 32∘, then what will the angle between incident ray and reflected ray?
To solve the problem of finding the angle between the incident ray and the reflected ray when the angle of incidence is given as 32∘, we can follow these steps:
1. Understand the Concept of Reflection:
- When a ray of light strikes a surface, it is called the incident ray. After striking the surface, it bounces back, which is called the reflected ray. The angle formed between the incident ray and the normal (an imaginary line perpendicular to the surface) is called the angle of incidence (i), and the angle formed between the reflected ray and the normal is called the angle of reflection (r).
2. Identify the Given Information:
- The angle of incidence (i) is given as 32∘.
3. Apply the Law of Reflection:
- According to the law of reflection, the angle of incidence is equal to the angle of reflection. Therefore, we can write:
i=r
- Since i=32∘, we can conclude that:
r=32∘
4. Calculate the Angle Between the Incident Ray and the Reflected Ray:
- The angle between the incident ray and the reflected ray can be found by adding the angle of incidence and the angle of reflection:
Angle between incident ray and reflected ray=i+r
- Substituting the values we have:
Angle=32∘+32∘=64∘
5. Final Answer:
- Therefore, the angle between the incident ray and the reflected ray is 64∘.
- When a ray of light strikes a surface, it is called the incident ray. After striking the surface, it bounces back, which is called the reflected ray. The angle formed between the incident ray and the normal (an imaginary line perpendicular to the surface) is called the angle of incidence (i), and the angle formed between the reflected ray and the normal is called the angle of reflection (r).
- The angle of incidence (i) is given as 32∘.
- According to the law of reflection, the angle of incidence is equal to the angle of reflection. Therefore, we can write:
i=r
- Since i=32∘, we can conclude that:
r=32∘
- The angle between the incident ray and the reflected ray can be found by adding the angle of incidence and the angle of reflection:
Angle between incident ray and reflected ray=i+r
- Substituting the values we have:
Angle=32∘+32∘=64∘
- Therefore, the angle between the incident ray and the reflected ray is 64∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The angle of incidence on a plane mirror is 30∘ . The angle between the incident ray and the reflected ray is
A30∘B15∘C60∘D90∘
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionName the following
The angle between the incident ray and the normal
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.
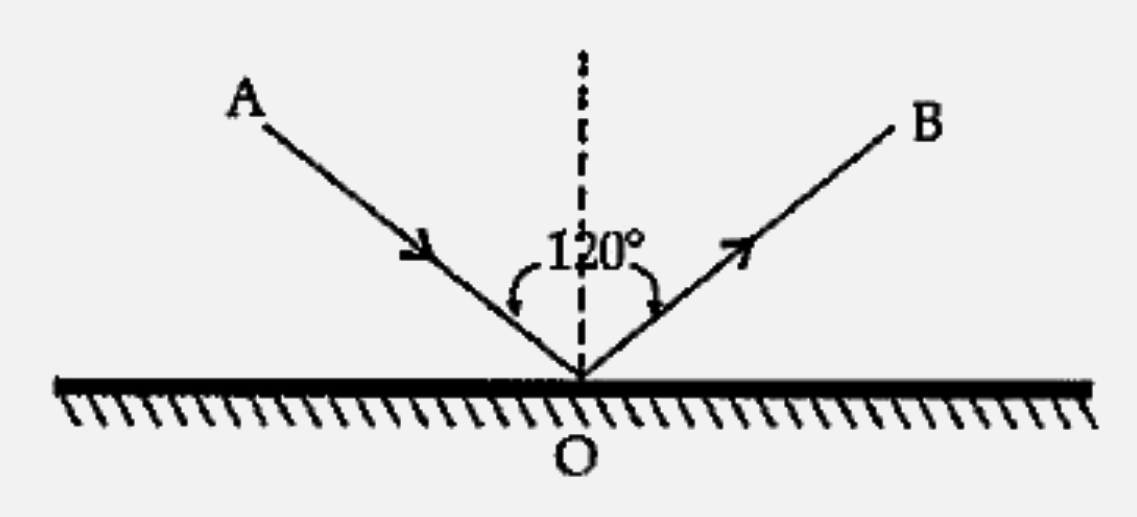
What is the value of the angle of reflection?
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.

If the image of an object is formed 5 cm behind the mirror, what is the distance between the image and the object?
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.

If two plane mirrors are used and kept facing parallel to each other, how many images are formed if the object is kept in between them?
View SolutionA plane mirror lies face up, making an angle of 15∘ with the horizontal .A ray of light shines down vertically on the mirror .What is the angle of incidence? What will be the angle between the reflection ray and the horizontal?
View Solution