If the angle of reflection is 45∘, what is the angle between the incident ray and the reflected ray?
To solve the problem of finding the angle between the incident ray and the reflected ray when the angle of reflection is 45∘, we can follow these steps:
1. Understand the Law of Reflection: According to the law of reflection, the angle of incidence (I) is equal to the angle of reflection (R). This can be expressed as:
I=R
2. Identify Given Information: The problem states that the angle of reflection is 45∘. Therefore, we can write:
R=45∘
3. Determine the Angle of Incidence: Since the angle of incidence is equal to the angle of reflection, we can conclude:
I=45∘
4. Calculate the Angle Between the Incident Ray and the Reflected Ray: The angle between the incident ray and the reflected ray can be found by adding the angle of incidence and the angle of reflection:
Angle between incident ray and reflected ray=I+R
Substituting the values:
=45∘+45∘=90∘
5. Conclusion: Therefore, the angle between the incident ray and the reflected ray is:
90∘
Final Answer:
The angle between the incident ray and the reflected ray is 90∘.
---
I=R
R=45∘
I=45∘
Angle between incident ray and reflected ray=I+R
Substituting the values:
=45∘+45∘=90∘
90∘
The angle between the incident ray and the reflected ray is 90∘.
Topper's Solved these Questions
- LIGHT ENERGYBook:ICSEChapter:LIGHT ENERGYExercise:EXERCISE (SECTION II) (Long answer question)
Explore 5 Videos
- LIGHT ENERGYBook:ICSEChapter:LIGHT ENERGYExercise:EXERCISE (PICTURE STUDY)
Explore 10 Videos
- LIGHT ENERGYBook:ICSEChapter:LIGHT ENERGYExercise:EXERCISE (SECTION II) (Distinguish between)
Explore 7 Videos
- HEATBook:ICSEChapter:HEATExercise:EXERCISE (PICTURE)
Explore 10 Videos
- MODEL TEST PAPER 1Book:ICSEChapter:MODEL TEST PAPER 1Exercise:SECTION II
Explore 43 Videos
Similar Questions
Knowledge Check
The angle of incidence on a plane mirror is 30∘ . The angle between the incident ray and the reflected ray is
A30∘B15∘C60∘D90∘Light is incident on a glass surface at polarising angle of 57.5∘ Then the angle between the incident ray and the refracted ray is
A57.5∘B115∘C205∘D145∘
Distinguish between Incident ray and reflected ray .
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.
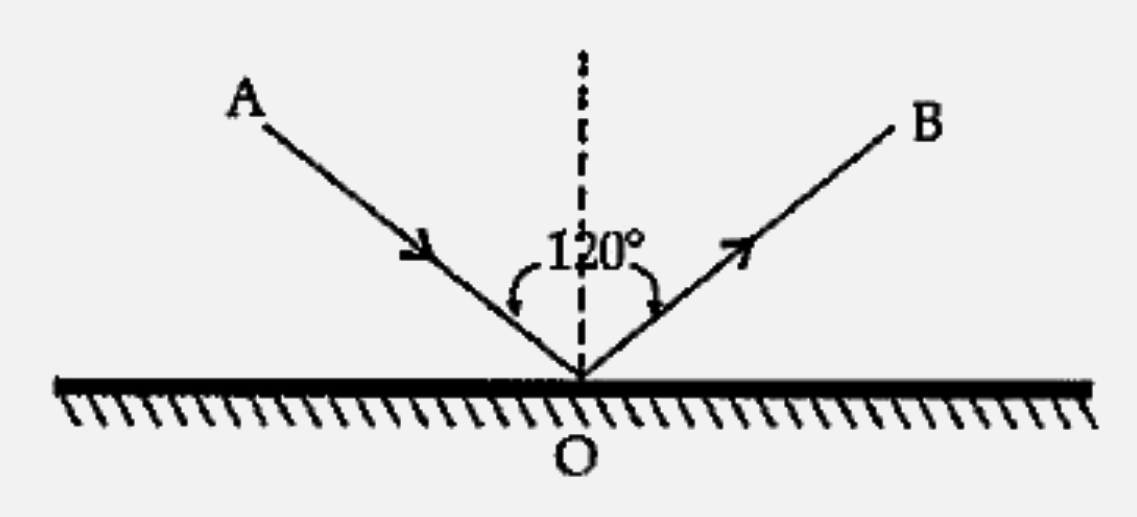
What is the value of the angle of reflection?
View SolutionA ray of light falls on a plane mirror. When the mirror is turned, about an axis at right angles to the plane of mirror by 20∘ the angle between the incident ray and new reflected ray is 45∘. The angle between the incident ray and original reflected ray was therefore.
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.

If the image of an object is formed 5 cm behind the mirror, what is the distance between the image and the object?
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.

If two plane mirrors are used and kept facing parallel to each other, how many images are formed if the object is kept in between them?
View SolutionAngle of reflection is the angle between the reflected ray and the ………………. incident ray/normal).
View Solution
