When a body moved along a straight line from A to B its velocity vector is represented by a straight line - directed from A to B . But " when the same body rotates in circular path is velocity vector is represented by a straight line perpendicular to the plane of the circular path " . Why ?
To understand the behavior of the velocity vector of a body moving in a straight line versus one moving in a circular path, let's break down the explanation step by step.
1. Understanding Velocity in Linear Motion:
- When a body moves from point A to point B in a straight line, its velocity vector can be represented as a straight line directed from A to B. This is because the velocity vector indicates the direction of motion and the magnitude of the speed. In this case, the velocity vector points directly along the path of motion.
2. Understanding Circular Motion:
- When the same body is tied to a wire and rotates in a circular path, its position changes continuously. Let's denote the position of the body at different instances as A, A', A'', A''', etc. As the body moves, it traces a circular path.
3. Velocity Vector in Circular Motion:
- In circular motion, the velocity vector at any point on the circular path is always tangent to the circle at that point. This means that if you were to draw a line that just touches the circle at the point where the body is located, that line represents the velocity vector.
4. Direction of the Velocity Vector:
- The velocity vector in circular motion is perpendicular to the radius of the circle at that point. This is because the motion is tangential to the circular path, and the radius points towards the center of the circle. Therefore, the velocity vector is not directed towards the center but rather along the tangent, which is perpendicular to the radius.
5. Centripetal Acceleration:
- In uniform circular motion, there is a centripetal acceleration directed towards the center of the circle. The velocity vector is always perpendicular to this acceleration. This relationship is crucial because it maintains the circular motion of the body.
6. Breaking the Wire:
- If the wire were to break at any point during the circular motion, the body would no longer be constrained to move in a circle. Instead, it would move in a straight line in the direction of the velocity vector at that moment. This illustrates that the velocity vector represents the direction of motion that the body would take if it were to continue moving without any constraints.
Summary:
- The velocity vector in linear motion is directed along the path of motion (A to B).
- In circular motion, the velocity vector is tangent to the circle and perpendicular to the radius, indicating the direction of motion at that point.
- The relationship between velocity and centripetal acceleration is key to understanding why the velocity vector behaves this way in circular motion.
- When a body moves from point A to point B in a straight line, its velocity vector can be represented as a straight line directed from A to B. This is because the velocity vector indicates the direction of motion and the magnitude of the speed. In this case, the velocity vector points directly along the path of motion.
- When the same body is tied to a wire and rotates in a circular path, its position changes continuously. Let's denote the position of the body at different instances as A, A', A'', A''', etc. As the body moves, it traces a circular path.
- In circular motion, the velocity vector at any point on the circular path is always tangent to the circle at that point. This means that if you were to draw a line that just touches the circle at the point where the body is located, that line represents the velocity vector.
- The velocity vector in circular motion is perpendicular to the radius of the circle at that point. This is because the motion is tangential to the circular path, and the radius points towards the center of the circle. Therefore, the velocity vector is not directed towards the center but rather along the tangent, which is perpendicular to the radius.
- In uniform circular motion, there is a centripetal acceleration directed towards the center of the circle. The velocity vector is always perpendicular to this acceleration. This relationship is crucial because it maintains the circular motion of the body.
- If the wire were to break at any point during the circular motion, the body would no longer be constrained to move in a circle. Instead, it would move in a straight line in the direction of the velocity vector at that moment. This illustrates that the velocity vector represents the direction of motion that the body would take if it were to continue moving without any constraints.
- The velocity vector in linear motion is directed along the path of motion (A to B).
- In circular motion, the velocity vector is tangent to the circle and perpendicular to the radius, indicating the direction of motion at that point.
- The relationship between velocity and centripetal acceleration is key to understanding why the velocity vector behaves this way in circular motion.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - VERY SHORT ANSWER QUESTIONS10videos
VECTORS SCALARS ELEMENTARY CALCULUS
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - SELECTED PROBLEMS (FROM VECTOR ADDITION )14videos
VECTORS SCALARS ELEMENTARY CALCULUS
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - LONG ANSWER QUESTIONS5videos
VECTORS SCALARS ELEMENTARY CALCULUS
- BOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (SELECTED PROBLEMS)38videos
UNITS
- BOOK - ICSECHAPTER - WAVESEXERCISE - From Musical Sound10videos
WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The equation ax+by+c=0 represents a straight line
Afor all real numbers a,b and cBonly when a≠0Conly where b≠0Donly when atleast one a and b is non - zero. - Question 2 - Select One
When a body moves in a circular path, outward force is called a ......
APseudo forceBCentrifugal forceCCentripetal forceDReaction force
A body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionTwo particles are moving along a straight line as shown. The velocity of approach between A and B is
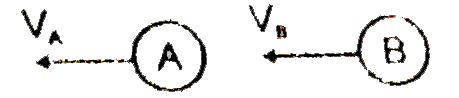 View Solution
View SolutionThe velocity versus time graph of a body moving in a straight line is as shown in the figure below
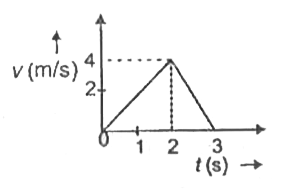 View Solution
View SolutionThe velocity time plot for a particle moving on straight line is shown in the figure.
 View Solution
View Solution

