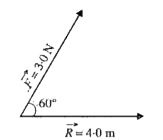
The vector →F is a force of 3.0 newton making an angle of 60∘ with the displacement . →R of magnitude 4.0 m , find
the magnitude and direction of the cross product →R×→F

6√3 Nm , directed perpendicular to
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - FROM UNIT VECTORS COMPONENTS OF A VECTOR
6 Videos
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (SELECTED PROBLEMS)
38 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - From Musical Sound
10 Videos
Similar Questions
The vector →F is a force of 3.0 newton making an angle of 60∘ with the displacement . →R of magnitude 4.0 m , find
the value of the dot product →F.→R
View SolutionA vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View Solution
Knowledge Check
The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8
→A is a vector with magnitude A, then the unit vector ˆA in the direction →A is
View SolutionIf →r is a vector of magnitude 21 and has direction ratios 2,−3and6, then find →r.
View SolutionIf →a and →b are two vectors of the same magnitude inclined at an angle of 600 such that →a.→b=8 write the value of their magnitude.
View SolutionWhat is the angle between vectors →a and →b with magnitudes 2 and 3 respectively ? Given →a.→b=√3 .
View SolutionTwo vectors →a and →b are at an angle of 60∘ with each other . Their resultant makes an angle of 45∘ with →a If ∣∣→b∣∣=2unit , then |→a| is
View SolutionThe angle between the vector →A and →B is θ. Find the value of triple product →A.(→B×→A).
View SolutionThe angle between the vector →A and →B is θ. Find the value of triple product →A.(→B×→A).
View Solution
