Two masses 7 kg and 12 kg are connected at the two ends of a metal wire that goes ove a frictionless puulley. What should be in the minimum radius of the wire in order that the wire does not break,if the breaking stess of the metal is 1.3×108N/m2 ?
To solve the problem, we need to find the minimum radius of the wire that will not break when two masses of 7 kg and 12 kg are connected over a frictionless pulley. The breaking stress of the metal wire is given as 1.3×108N/m2.
1. Identify the Forces Acting on the System:
- The two masses are m1=7kg and m2=12kg.
- The weight of each mass can be calculated using W=mg, where g=9.8m/s2.
- The tension in the wire will be influenced by the heavier mass, which will be m2.
2. Calculate the Weight of Each Mass:
- Weight of m1:
W1=m1⋅g=7kg⋅9.8m/s2=68.6N
- Weight of m2:
W2=m2⋅g=12kg⋅9.8m/s2=117.6N
3. Determine the Tension in the Wire:
- The tension T in the wire when the system is in equilibrium can be expressed as:
T=W2−W1=117.6N−68.6N=49N
4. Use the Breaking Stress Formula:
- The breaking stress σ is given by:
σ=TA
- Where A is the cross-sectional area of the wire, given by A=πr2.
- Rearranging gives:
T=σ⋅A=σ⋅πr2
- Therefore:
r2=Tσ⋅π
5. Substitute the Values:
- Substitute T=49N and σ=1.3×108N/m2:
r2=491.3×108⋅π
- Using π≈3.14:
r2=491.3×108⋅3.14≈494.082×108≈1.2×10−7m2
6. Calculate the Radius:
- Taking the square root to find r:
r=√1.2×10−7≈3.46×10−4m=0.346mm
Final Answer:
The minimum radius of the wire should be approximately 0.346mm.
- The two masses are m1=7kg and m2=12kg.
- The weight of each mass can be calculated using W=mg, where g=9.8m/s2.
- The tension in the wire will be influenced by the heavier mass, which will be m2.
- Weight of m1:
W1=m1⋅g=7kg⋅9.8m/s2=68.6N
- Weight of m2:
W2=m2⋅g=12kg⋅9.8m/s2=117.6N
- The tension T in the wire when the system is in equilibrium can be expressed as:
T=W2−W1=117.6N−68.6N=49N
- The breaking stress σ is given by:
σ=TA
- Where A is the cross-sectional area of the wire, given by A=πr2.
- Rearranging gives:
T=σ⋅A=σ⋅πr2
- Therefore:
r2=Tσ⋅π
- Substitute T=49N and σ=1.3×108N/m2:
r2=491.3×108⋅π
- Using π≈3.14:
r2=491.3×108⋅3.14≈494.082×108≈1.2×10−7m2
- Taking the square root to find r:
r=√1.2×10−7≈3.46×10−4m=0.346mm
The minimum radius of the wire should be approximately 0.346mm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2 (SOLVED EXAMPLES)22videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (SOLVED EXAMPLES)31videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D12videos
SAMPLE QUESTION PAPER - 01
Similar Questions
Two blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109Nm−2. What should be the minimum radius of the wire used if it is not to break? Take g=10ms−2
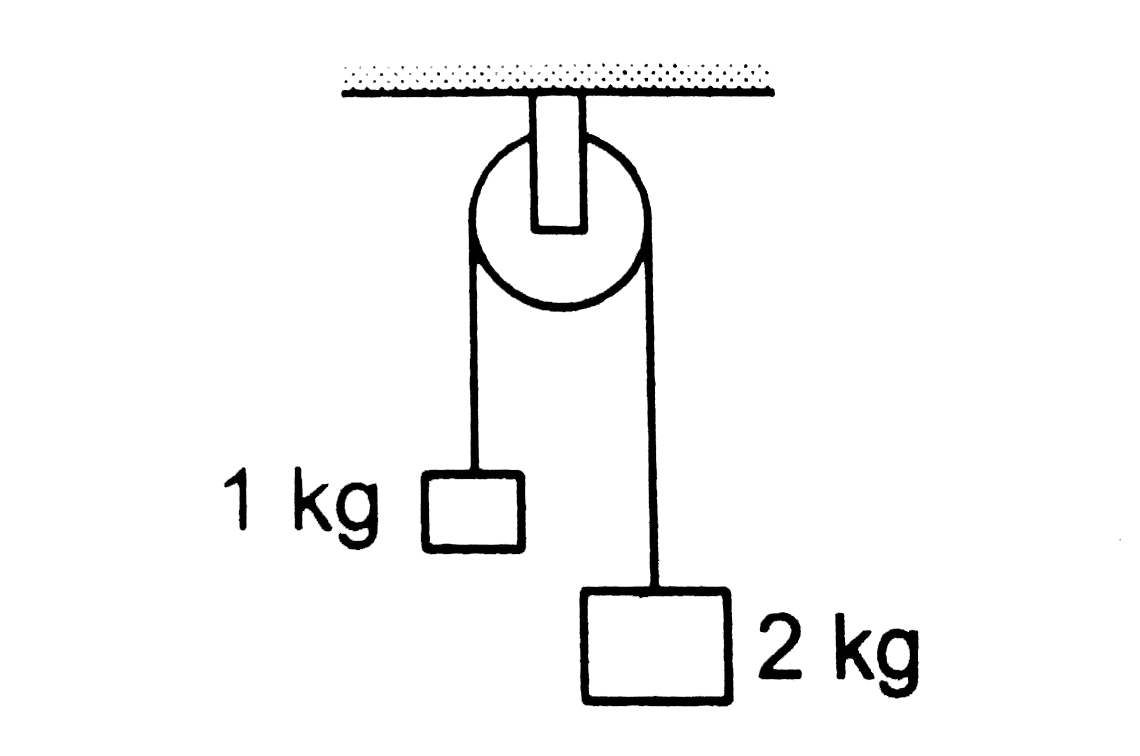 View Solution
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
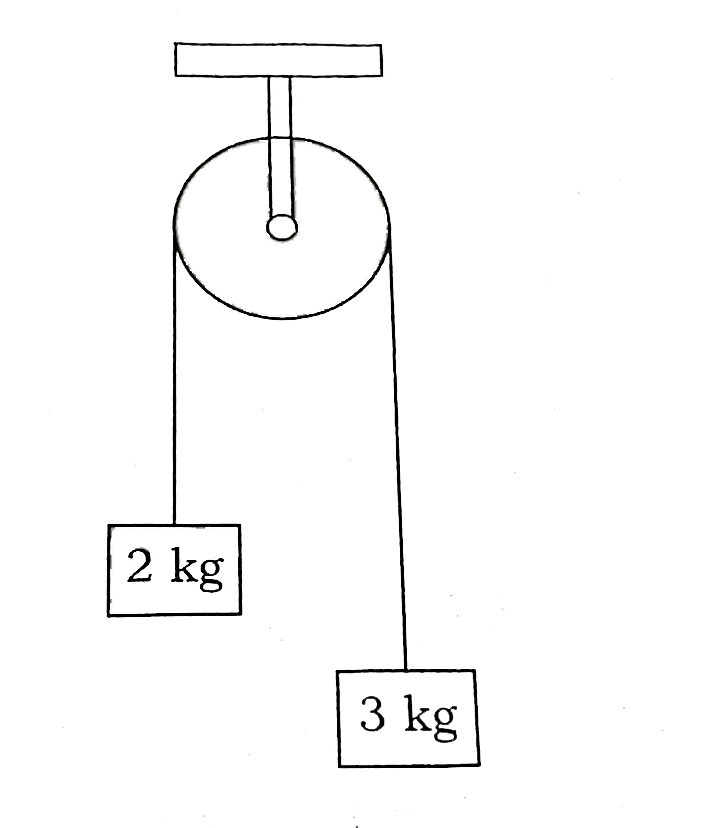 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 A0.5 mmB1 mmC1.5 mmD2 mm
A0.5 mmB1 mmC1.5 mmD2 mm
Two block of mass m and M are connected means of a metal of a metal wire passing over a frictionless fixed pulley. The area of cross section of the wire is 6.67×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg. Find the maximum value of M in kg for which the wire will not break. (g=10m/s2).
View SolutionA wire of mass 5 gm is kept horizontally on the surface of water. What ist he minimum length of the wire so that it does not break the surface film.Surface tension =72×10−3N/m
View SolutionTwo bodies of masses 2kg and 3kg are connected by a metel wire of cross section 0.04 mm2. Breaking stress of metel wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is :
 View Solution
View SolutionBreaking stress for a material is 2×108N/m2. What maximum length of the wire of this material can be taken t the wire does not break by own weight? Density of material = 5×103kg/m3
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 View Solution
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
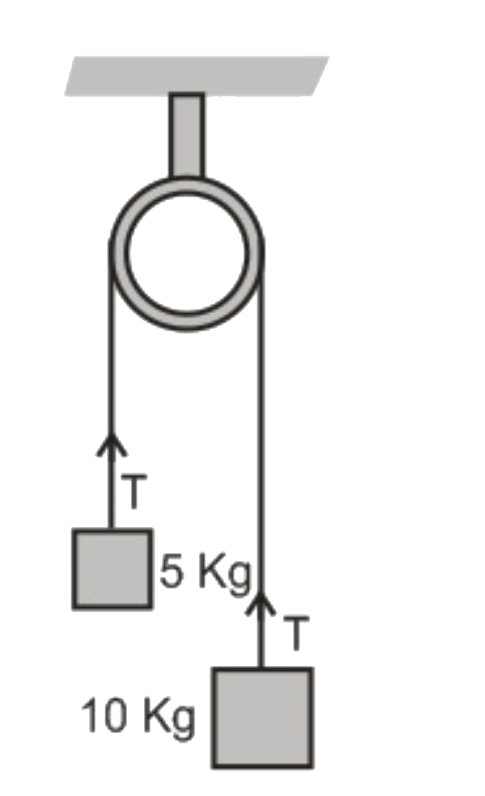 View Solution
View SolutionA copper wire of negligible mass, 1m length and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed. A ball of mass 1kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20rad/s. If the elongation in the wire is 10−3m.
a. Find the Young's modulus of the wire (in terms of ×1011N/m2).
b. If for the same wire as stated above, the angular velocity is increased to 100rad/s and the wire breaks down, find the breaking stress (in terms of ×1010N/m2).View Solution

