A steel wire of diameter 0.8 mm and length 1m is clamped firmly at two points P and Q which are one metre apart and in the same horizontal plane. A body is hung from the middle point of the wire, such that the middle point sags one cm lower from the original position as shown in figure. Calculate the mass of the body. Y=2×1011N/m2.
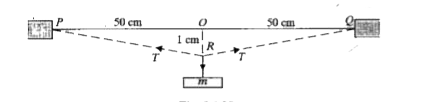
Let T be the tension in each segment of the wire and ∠ORQ=∠ORP=θ
2Tcosθ=mg
Stress =TA, T = Stress ×A
T=Y× Strain ×A
A=πd2/4
From the triangle POR, PR=√PO2+OR2=√2500+1=50.01cm
Final length of the wire =50.01+50.01=100.02cm
Original length =100cm
Change in length = 0.02cm
Strain =0.02100=2×10−4
T=Y× Strain ×A
=2×1011×2×10−4×3.14×(0.8×10−3)24
= 20.096N
m=2Tcosθg=2×20.096×19.8×50.01=0.082kg
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2 (SOLVED EXAMPLES)22videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (SOLVED EXAMPLES)31videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D12videos
SAMPLE QUESTION PAPER - 01
Similar Questions
The moment of inertia of a uniform rod of mass 0.50 kg and length 1 m is 0.10 kg m^2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to
View Solution
Knowledge Check
- Question 1 - Select One
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2rev./s at the bottom of the circle. The cross-sectional area of the wire is 0.065cm2 . Calculate the elongation of the wire when the mass is at the lowest point of its path Ysteel=2×1011Nm−2.
A0.52 mmB1.52 mmC2.52 mmD3.52 mm
A steel wire of original length 1m and cross-sectional area 4.00mm2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16kg is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel =2.0×1011Nm−2. Take g=10ms−2View SolutionA steel wire of negligible mass, length 2I, cross sectional area 'A' and Young's modulus 'Y' is held between two rigid walls. A small body of mass 'm' is suspended from its middle point 'O' as shown. The vertical descent of the middle point 'O' of the wire is
 View Solution
View SolutionA wire of cross section A is stretched horizontally between two clamps located 2lm apart. A weight Wkg is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance x<l, the strain produced is
View SolutionA steel wire of mass μ per unit length with a circular cross-section has a radius of 0.1cm. The wire is of length 10m when measured lying horizontal, and hangs from a hook on the wall. A mass fo 25kg is hung from the free end of the wire. Assume the wire to be uniform and laterla strain << logitudinal strain. If density of steel is 7860kgm−3 and Young's modulus is 2×1011N/m2 then the extension in the length fo the wire is
View SolutionA 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2rev./s at the bottom of the circle. The cross-sectional area of the wire is 0.065cm2 . Calculate the elongaton of the wire when the mass is at the lowest point of its path Ysteel=2×1011Nm−2.
View SolutionFind the net vertical displacement of point O, when a mass of 2.5 kg is suspended from the mid-point O of the rod shown (Y=2×1011N/m2).
 View Solution
View SolutionA sphere of radius 10cm and mass 25 kg is attached to the lower end of a steel wire of length 5m and diameter 4mm which is suspended from the ceiling of a room . The point of support is 521cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Ysteel=2×1011N/m2).
View Solution
