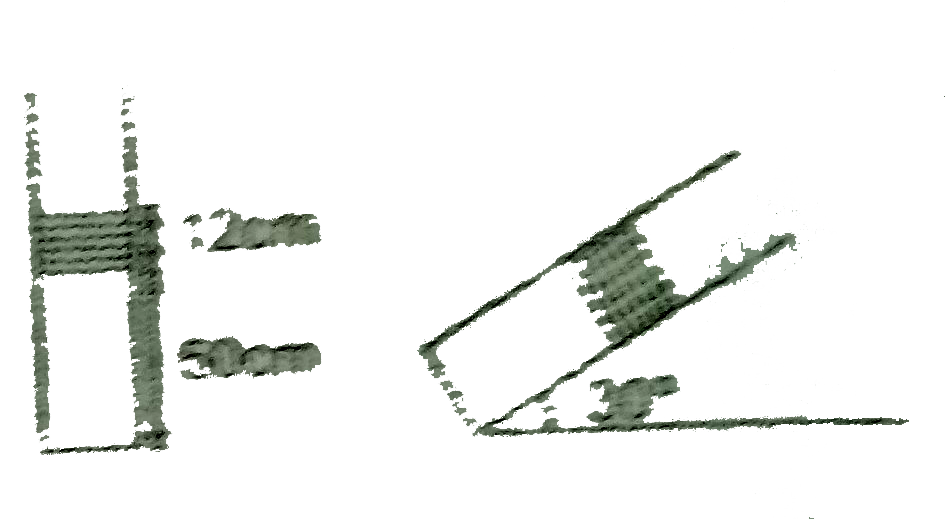
A thin tube sealed at both ends is 90 cm long. It is kept horizontally, the middle 10cm containing mercury and the two equal ends containing air at standard atmospheric pressure. The tube is turned and kept in vertical position. By what amount will the mercury be displaced?

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of how much the mercury will be displaced when the tube is turned from a horizontal to a vertical position, we can follow these steps:
1. Understand the Setup:
- The tube is 90 cm long, with 10 cm of mercury in the middle.
- The remaining 80 cm is filled with air at standard atmospheric pressure (76 cm of mercury).
2. Identify the Lengths:
- When the tube is horizontal, the mercury occupies the middle 10 cm, leaving 40 cm of air on each side (total length = 90 cm).
- In vertical position, the mercury will fall due to gravity, causing a displacement.
3. Define Variables:
- Let $X$ be the amount of mercury displaced downwards.
- The height of air column in chamber A becomes $40 + X$ cm.
- The height of air column in chamber B becomes $40 - X$ cm.
4. Apply Boyle's Law:
- For chamber A (initially at 40 cm of air):
$P_{A} \cdot V_{A} = P_{A} \cdot (A \cdot (40 + X))$
where $P_{A}$ is the pressure in chamber A.
- For chamber B (initially at 40 cm of air):
$P_{B} \cdot V_{B} = P_{B} \cdot (A \cdot (40 - X))$
where $P_{B}$ is the pressure in chamber B.
5. Set Up the Equations:
- The initial pressure in both chambers is atmospheric pressure (76 cm of mercury):
$P_{A} = \frac{76 \cdot 40}{40 + X} (for chamber A)$
$P_{B} = \frac{76 \cdot 40}{40 - X} (for chamber B)$
6. Pressure Balance:
- The pressure in chamber B must balance the pressure from the mercury and chamber A:
$P_{B} = P_{H g} + P_{A}$
- The pressure due to mercury is $P_{H g} = ρ g h$ , where $h = 10$ cm (the height of mercury).
7. Combine the Equations:
- Substitute the expressions for $P_{A}$ and $P_{B}$ into the balance equation:
$\frac{76 \cdot 40}{40 - X} = \frac{76 \cdot 40}{40 + X} + 76$
8. Solve for X:
- Rearranging and simplifying leads to a quadratic equation:
$680 X + 5776 X^{2} - 121600 = 0$
- Use the quadratic formula to solve for $X$ :
$X = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
- Substituting $a = 5776, b = 680, c = - 121600$ yields:
$X \approx 4.09 cm$
Final Answer:
The mercury will be displaced by approximately 4.09 cm when the tube is turned to a vertical position.

Updated on:18/9/2024

A thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of $60^{\circ}$ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at $30^{\circ} C$ ).
A $75.4$
B $45.8$
C $67.5$
D $89.3$