if p represents radiation pressure, c represent speed of light and Q represents radiation energy striking a unit area per second, then non-zero integers x,y and z such that pxQycz is dimensionless are.
x=1,y=1,z=−1
x=1,y=−1,z=1
x=−1,y=1,z=1
x=1,y=1,z=1
The correct Answer is:b
PxQyCz is dimensional when [ML−1T−2]x[ML2T−2/L2T]y[LT−1]z=M0L0T0 solving x=1, y = 1, z = 1.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - VECTORS AND SCALARS [Selected from Previoius Years Engg. & Med. & IIT Exam Qns]35videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics (UNIFORMLY ACCELERATED MOTION)58videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
If P represents radiation pressure , C represents the speed of light , and Q represents radiation energy striking a unit area per second , then non - zero integers x,y,z such that PxQyCz is dimensionless , find the values of x,y,andz.
View SolutionIf P represents radiation pressure , C represents the speed of light , and Q represents radiation energy striking a unit area per second , then non - zero integers x,y,z such that PxQyCz is dimensionless , find the values of x,y,andz.
View SolutionIf P represents radiation pressure , C represents the speed of light , and Q represents radiation energy striking a unit area per second , then non - zero integers x,y,z such that PxQyCz is dimensionless , find the values of x,y,andz.
View SolutionLet P represent radiation pressure, c represent speed of light and l represents radiation energy striking a unit area per second, then PxIycz will be dimensionless for
View SolutionIf P represents radiation pressure, C speed of light, and Q radiation energy striking unit area per second and x,y,z are non zero integers, then P^x Q^y C^z is dimensionless. The values of X,y and z are respectively
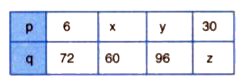
View SolutionIf p and q vary inversely, find the values of x,y and z.
 View Solution
View SolutionIf p and q vary inversely, find the values of x,y and z.
 View Solution
View SolutionIn Argand diagram, O,P,Q represent the origin, z and z+iz respectively then ∠OPQ=
View SolutionIn Argand diagram, O, P, Q represent the origin, z and z+ iz respectively then ∠OPQ=
View SolutionIF p and q are in direct variation of x, y and z in the table given below:
 View Solution
View Solution

