Two stones are thrown from the same point with velocity of 5 ms−1 one vertically upwards and the other vertically downwards. When the first stone is at the highest point the relative velocity of the second stone with respect to the first stone is,
5ms−1
0ms−1
10ms−1
−5ms−1
The correct Answer is:c
To solve the problem, we need to determine the relative velocity of the second stone (thrown downwards) with respect to the first stone (thrown upwards) when the first stone reaches its highest point.
1. Identify the Initial Conditions:
- The first stone (Stone A) is thrown upwards with an initial velocity uA=5ms−1.
- The second stone (Stone B) is thrown downwards with an initial velocity uB=−5ms−1 (negative because it is in the downward direction).
2. Determine the Time Taken for Stone A to Reach the Highest Point:
- At the highest point, the final velocity vA=0.
- We can use the equation of motion:
vA=uA+aAt
where aA=−10ms−2 (acceleration due to gravity acting downwards).
- Substituting the values:
0=5−10t
Rearranging gives:
10t=5⟹t=510=0.5s
3. Calculate the Velocity of Stone B at t=0.5s:
- We use the same equation of motion for Stone B:
vB=uB+aBt
where aB=−10ms−2.
- Substituting the values:
vB=−5−10(0.5)
vB=−5−5=−10ms−1
4. Determine the Relative Velocity:
- The relative velocity of Stone B with respect to Stone A is given by:
vBA=vB−vA
- Since vA=0 at the highest point:
vBA=−10−0=−10ms−1
- The magnitude of the relative velocity is 10ms−1.
5. Conclusion:
- The relative velocity of the second stone with respect to the first stone when the first stone is at the highest point is 10ms−1.
Final Answer:
The relative velocity of the second stone with respect to the first stone is 10ms−1.
- The first stone (Stone A) is thrown upwards with an initial velocity uA=5ms−1.
- The second stone (Stone B) is thrown downwards with an initial velocity uB=−5ms−1 (negative because it is in the downward direction).
- At the highest point, the final velocity vA=0.
- We can use the equation of motion:
vA=uA+aAt
where aA=−10ms−2 (acceleration due to gravity acting downwards).
- Substituting the values:
0=5−10t
Rearranging gives:
10t=5⟹t=510=0.5s
- We use the same equation of motion for Stone B:
vB=uB+aBt
where aB=−10ms−2.
- Substituting the values:
vB=−5−10(0.5)
vB=−5−5=−10ms−1
- The relative velocity of Stone B with respect to Stone A is given by:
vBA=vB−vA
- Since vA=0 at the highest point:
vBA=−10−0=−10ms−1
- The magnitude of the relative velocity is 10ms−1.
- The relative velocity of the second stone with respect to the first stone when the first stone is at the highest point is 10ms−1.
The relative velocity of the second stone with respect to the first stone is 10ms−1.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics (PROJECTILE MOTION)
31 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( Laws of motion )
36 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - VECTORS AND SCALARS [Selected from Previoius Years Engg. & Med. & IIT Exam Qns]
35 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
Two bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
View SolutionA stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-
View Solution
Knowledge Check
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone with respect to the first is shown in the figure. The equation of the linear part is
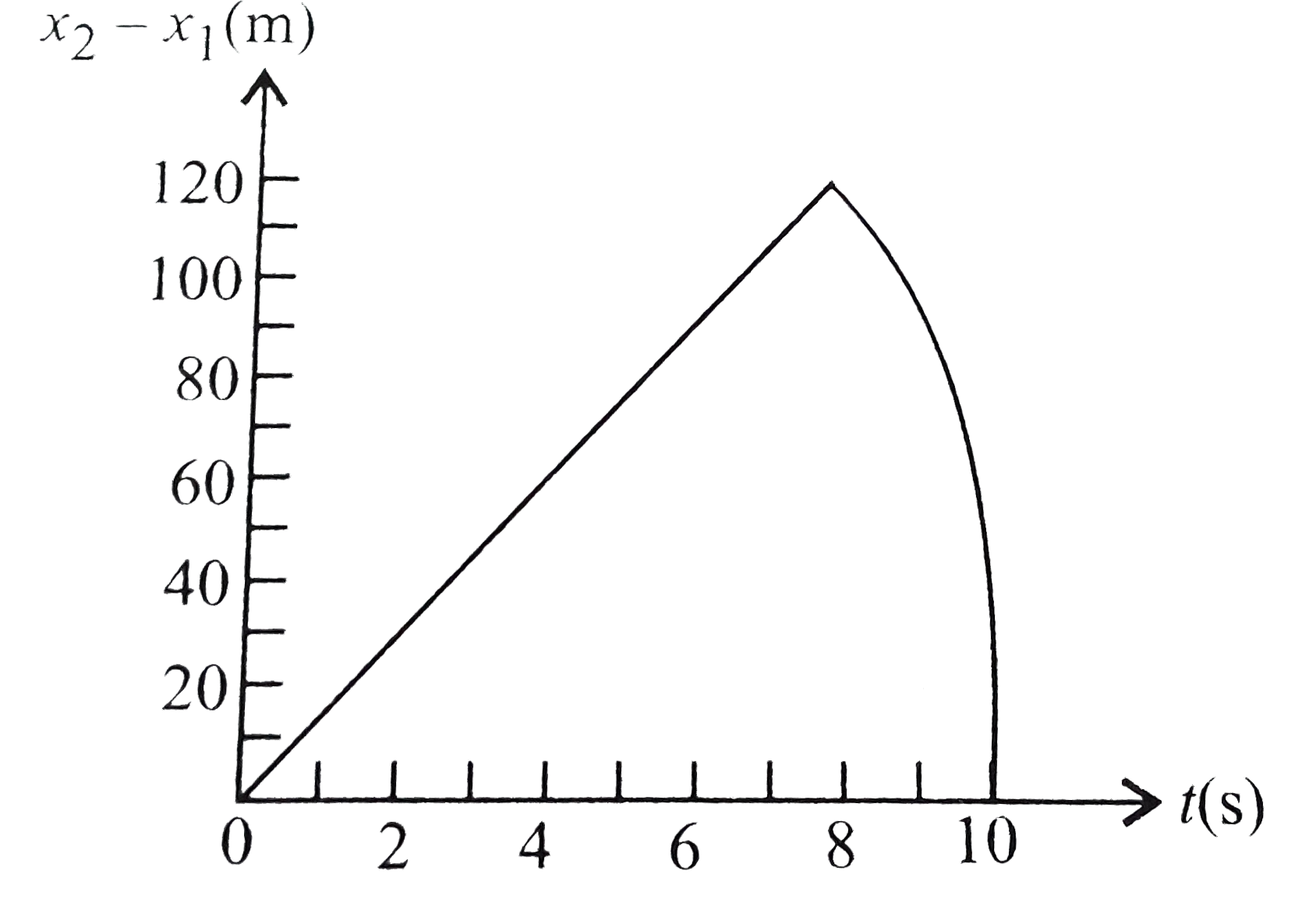 Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20tA stone is thrown horizontally with velocity u. The velocity of the stone 0.5 s later is 3u/2. The value of u is
A2.2ms−1B3.3ms−1C4.4ms−1D1.1ms−1A stone is thrown vertically upwards with an initial velocity u form the top of a tower, recahes the ground with a velocity 3u. The height of the tower is
A3u2gB4u2gC6u2gD9u2g
A ball is thrown vertically upward. What is the magnitude of velocity at the highest point ?
View SolutionA stone is thrown upwards with velocity 25m/s. Another stone is simultaneously thrown downward from the same point with speed 10 m/s. When the first stone is at a height 10 m. what is the relative velocity of first stone w.r.t second ?
View SolutionTwo stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u1=30m/sec and u2=50m/sec. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
(x2−x1) = the relative position of second stone with respect to first with time (t)
(v2−v1) = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.
View SolutionA stone is projected with speed of 50ms−1 at an angle of 60∘ with the horizontal. The speed of the stone at highest point of trajectory is
View SolutionA stone of mass 1kg is tied with a string and it is whirled in a vertical circle of radius 1 m. If tension at the highest point is 14 N, then velocity at lowest point will be
View Solution
