Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed and . Which of the curve represent correct variation (for the time interval in which both reach the ground) of
= the relative position of second stone with respect to first with time (t)
= the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.
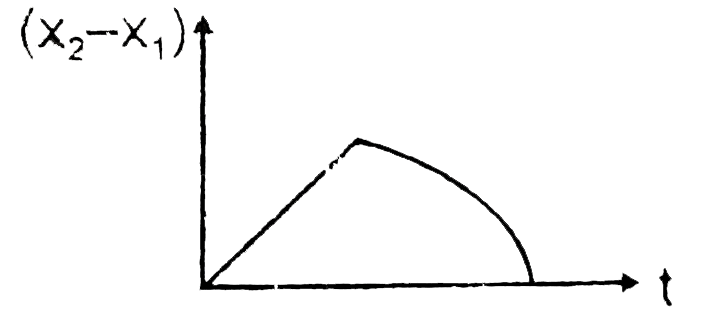


The correct Answer is:A, D
To solve the problem, we need to analyze the motion of the two stones thrown vertically upwards with different initial velocities. We will derive the expressions for the relative position and relative velocity of the two stones over time.
Step 1: Determine the equations of motion for both stones.
The equations of motion for an object thrown vertically upwards are given by:
x(t)=ut+12at2
where u is the initial velocity, a is the acceleration (which is −g for upward motion, where g≈9.81m/s2), and t is the time.
For the first stone (with initial speed u1=30m/s):
x1(t)=u1t−12gt2=30t−12(9.81)t2
For the second stone (with initial speed u2=50m/s):
x2(t)=u2t−12gt2=50t−12(9.81)t2
Step 2: Calculate the relative position x2−x1.
Now, we find the relative position of the second stone with respect to the first:
x2−x1=(50t−12(9.81)t2)−(30t−12(9.81)t2)
x2−x1=(50t−30t)=20t
Step 3: Analyze the relative position over time.
The relative position x2−x1 is directly proportional to time t. This means that as time increases, the difference in position increases linearly.
Step 4: Determine the equations for the velocities.
The velocities of the stones at any time t can be calculated using:
v(t)=u+at
For the first stone:
v1(t)=u1−gt=30−9.81t
For the second stone:
v2(t)=u2−gt=50−9.81t
Step 5: Calculate the relative velocity v2−v1.
Now, we find the relative velocity of the second stone with respect to the first:
v2−v1=(50−9.81t)−(30−9.81t)
v2−v1=50−30=20
Step 6: Analyze the relative velocity over time.
The relative velocity v2−v1 is constant at 20m/s. This means that the difference in velocities does not change over time.
Conclusion:
1. The relative position x2−x1 varies linearly with time t and can be represented by a straight line graph.
2. The relative velocity v2−v1 is constant over time and can be represented by a horizontal line graph.
x(t)=ut+12at2
where u is the initial velocity, a is the acceleration (which is −g for upward motion, where g≈9.81m/s2), and t is the time.
x1(t)=u1t−12gt2=30t−12(9.81)t2
x2(t)=u2t−12gt2=50t−12(9.81)t2
x2−x1=(50t−12(9.81)t2)−(30t−12(9.81)t2)
x2−x1=(50t−30t)=20t
v(t)=u+at
v1(t)=u1−gt=30−9.81t
v2(t)=u2−gt=50−9.81t
v2−v1=(50−9.81t)−(30−9.81t)
v2−v1=50−30=20
2. The relative velocity v2−v1 is constant over time and can be represented by a horizontal line graph.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.19
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.20
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.17
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff with initial speed vand2v. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
View Solution
Knowledge Check
Two stones are thrown from the same point with velocity of 5 ms−1 one vertically upwards and the other vertically downwards. When the first stone is at the highest point the relative velocity of the second stone with respect to the first stone is,
A5ms−1B0ms−1C10ms−1D−5ms−1Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone with respect to the first is shown in the figure. The equation of the linear part is
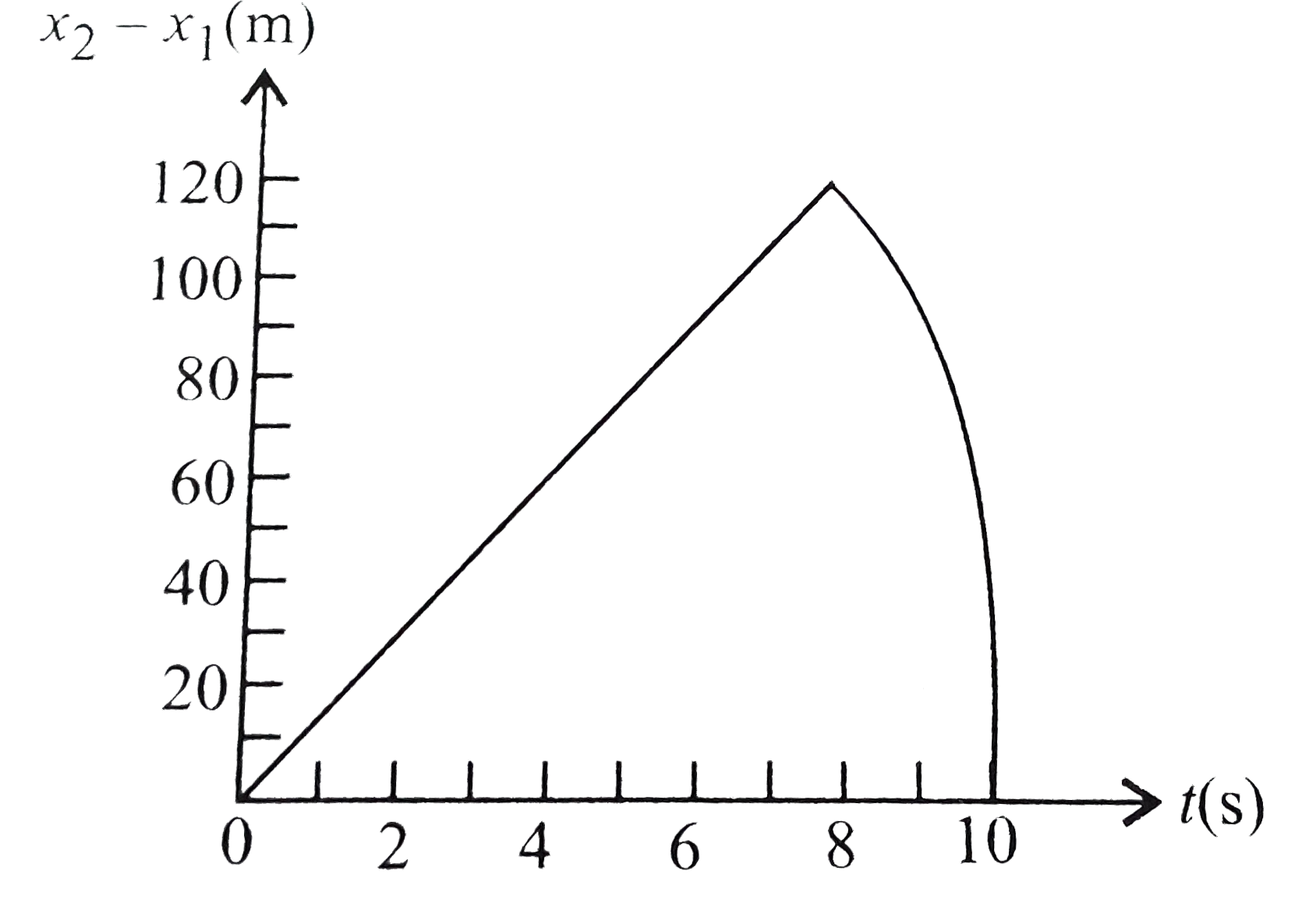 Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20tA stone is thrown vertically upwards with an initial velocity u form the top of a tower, recahes the ground with a velocity 3u. The height of the tower is
A3u2gB4u2gC6u2gD9u2g
A stone is thrown vertically upwards with an initial speed u from the top of a tower, reaches the ground with a speed 3u. The height of the tower is :
View SolutionTwo stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
View SolutionA ball is thrown vertically upward with a velocity u from the top of a tower. If it strikes the ground with velocity 3u, the time taken by the ball to reach the ground is
View SolutionA stone thrown upward with a speed u from the top of a tower reaches the ground with a velocity 4u. The height of the tower is
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
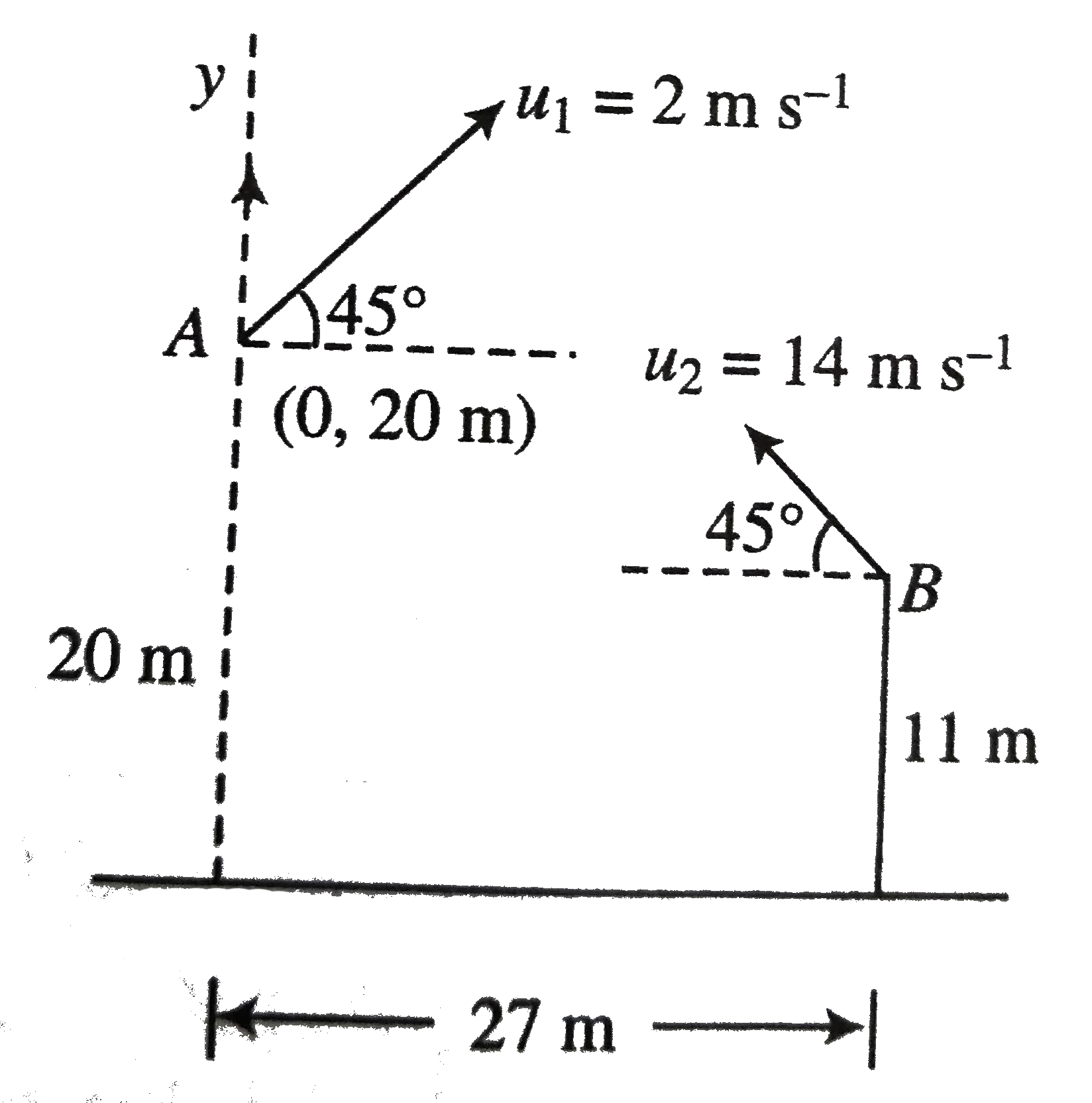
The relative velocity of B as seen from A in
View Solution
