A person slides freely down a frictionless inclined plane while his bag falls down vertically from the same height. The final speed of man and the bag should be such that
they depen on masses
The correct Answer is:b
To solve the problem of comparing the final speeds of a person sliding down a frictionless inclined plane and a bag falling vertically from the same height, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Define the scenario
- A person slides down a frictionless inclined plane from height h.
- A bag falls vertically from the same height h.
Step 2: Analyze the motion of the person
- For the person sliding down the inclined plane, we apply the conservation of mechanical energy:
Initial Potential Energy=Final Kinetic Energy
- The initial potential energy (PE) of the person at height h is given by:
PEinitial=mgh
(where m is the mass of the person and g is the acceleration due to gravity).
- The initial kinetic energy (KE) is zero because the person starts from rest:
KEinitial=0
- The final kinetic energy when the person reaches the bottom of the incline is:
KEfinal=12mv2m
- Setting the initial potential energy equal to the final kinetic energy:
mgh=12mv2m
Step 3: Simplify the equation for the person
- Cancel the mass m from both sides (since it appears in every term):
gh=12v2m
- Rearranging gives:
v2m=2gh
- Taking the square root:
vm=√2gh
Step 4: Analyze the motion of the bag
- For the bag falling vertically, we again apply the conservation of mechanical energy:
Initial Potential Energy=Final Kinetic Energy
- The initial potential energy of the bag is also:
PEinitial=mbgh
(where mb is the mass of the bag).
- The initial kinetic energy is zero:
KEinitial=0
- The final kinetic energy when the bag reaches the ground is:
KEfinal=12mbv2b
- Setting the initial potential energy equal to the final kinetic energy:
mbgh=12mbv2b
Step 5: Simplify the equation for the bag
- Cancel the mass mb from both sides:
gh=12v2b
- Rearranging gives:
v2b=2gh
- Taking the square root:
vb=√2gh
Step 6: Compare the speeds
- From the calculations, we have:
vm=√2gh
vb=√2gh
- Therefore, we conclude that:
vm=vb
Final Answer
The final speeds of the man and the bag are equal:
vm=vb
---
- A person slides down a frictionless inclined plane from height h.
- A bag falls vertically from the same height h.
- For the person sliding down the inclined plane, we apply the conservation of mechanical energy:
Initial Potential Energy=Final Kinetic Energy
- The initial potential energy (PE) of the person at height h is given by:
PEinitial=mgh
(where m is the mass of the person and g is the acceleration due to gravity).
KEinitial=0
KEfinal=12mv2m
mgh=12mv2m
- Cancel the mass m from both sides (since it appears in every term):
gh=12v2m
v2m=2gh
vm=√2gh
- For the bag falling vertically, we again apply the conservation of mechanical energy:
Initial Potential Energy=Final Kinetic Energy
- The initial potential energy of the bag is also:
PEinitial=mbgh
(where mb is the mass of the bag).
KEinitial=0
KEfinal=12mbv2b
mbgh=12mbv2b
- Cancel the mass mb from both sides:
gh=12v2b
v2b=2gh
vb=√2gh
- From the calculations, we have:
vm=√2gh
vb=√2gh
vm=vb
The final speeds of the man and the bag are equal:
vm=vb
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( WORK POWER ENERGY )35videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - FRICTION22videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics (PROJECTILE MOTION)31videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
A man is slipping on a frictions inclined plane & a bag falls down from the same height. Then the speed of both is related as:
View SolutionA particle starts sliding down a frictionless inclined plane. If Sn is the distance travelled by it from time t=n−1sec, to t=nsec, the ratio Snsn+1 is
View Solution
Knowledge Check
- Question 1 - Select One
A box of mass m slides down a frictionless inclined plane of length L and vertical height h. what is the change in its gravitational potential energy?
A−mgLB−mghC−mgL/hD−mgh/L - Question 2 - Select One
A block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
A5m/sB6m/sC8m/sD9m/s
A particle starts sliding down a frictionless inclined plane. If Sn is the distance travelled by it from time t=n−1sec, to t=nsec, the ratio Snsn+1 is
View SolutionA block slides down a smooth inclined placne when released from the top, while another falls freely from the same point. Which of the following is/are correct ?
View SolutionA box of dimentsion H×B×R is kept on a frictionless inclined plane as shown in the figure. A stone is thrown from one corner P with speed u parallel to the ceiling of the box such that it hits the floor of the box. At the same instant, the box is released to slide down the plane. Calculate the time of flight.
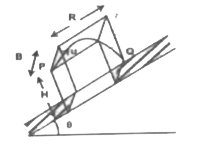 View Solution
View SolutionThe speed of a homogenous solid sphere after rolling down an inclined plane of vertical height h, from rest without sliding is
View SolutionThe speed of a uniform solid cylinder after rolling down an inclined plane of vertical height H, from rest without sliding is :-
View Solution(a) Show that the velocity acquired by a particle in sliding down an inclined plane is the same as that acquired by a particle falling freely from frst though a distance equal to the height of the inclined plane. (b) Find the time taken in sliding a particle down the whole length of the incline.
View Solution

