(a) Show that the velocity acquired by a particle in sliding down an inclined plane is the same as that acquired by a particle falling freely from frst though a distance equal to the height of the inclined plane. (b) Find the time taken in sliding a particle down the whole length of the incline.
To solve the problem, we will break it down into two parts as given in the question.
Part (a): Show that the velocity acquired by a particle in sliding down an inclined plane is the same as that acquired by a particle falling freely from a height equal to the height of the inclined plane.
1. Identify the height (h): Let the height of the inclined plane be h and the angle of inclination be θ.
2. Free fall case: For a particle falling freely from a height h, we can use the principle of conservation of energy. The potential energy at the height h is converted into kinetic energy just before it hits the ground.
- Initial potential energy: PE=mgh
- Final kinetic energy: KE=12mv2
- Setting them equal gives:
mgh=12mv2
- Cancelling m from both sides and rearranging gives:
v2=2gh⇒v1=√2gh
3. Inclined plane case: Now consider the particle sliding down the inclined plane. The acceleration of the particle down the incline is given by the component of gravitational acceleration along the incline:
- a=gsinθ
- Using the equation of motion v2=u2+2as where u=0 (initial velocity), a=gsinθ, and s=L (length of incline):
v2=0+2(gsinθ)L
4. Relate the length L to height h: From the geometry of the inclined plane, we have:
h=Lsinθ⇒L=hsinθ
5. Substituting L into the velocity equation:
v2=2(gsinθ)(hsinθ)
- Simplifying this gives:
v2=2gh
- Therefore, the velocity acquired by the particle sliding down the incline is:
v2=√2gh
6. Conclusion: Since v1=v2, we have shown that the velocity acquired by a particle in sliding down an inclined plane is the same as that acquired by a particle falling freely from a height equal to the height of the inclined plane.
Part (b): Find the time taken in sliding a particle down the whole length of the incline.
1. Use the equation of motion: We will use the equation:
s=ut+12at2
- Here, s=L, u=0, and a=gsinθ:
L=0⋅t+12(gsinθ)t2
- This simplifies to:
L=12gsinθ⋅t2
2. Substituting L: We already know L=hsinθ:
hsinθ=12gsinθ⋅t2
3. Rearranging for t2:
t2=2hgsin2θ
4. Taking the square root:
t=√2hgsin2θ
5. Conclusion: The time taken to slide down the whole length of the incline is:
t=√2hgsin2θ
- Initial potential energy: PE=mgh
- Final kinetic energy: KE=12mv2
- Setting them equal gives:
mgh=12mv2
- Cancelling m from both sides and rearranging gives:
v2=2gh⇒v1=√2gh
- a=gsinθ
- Using the equation of motion v2=u2+2as where u=0 (initial velocity), a=gsinθ, and s=L (length of incline):
v2=0+2(gsinθ)L
h=Lsinθ⇒L=hsinθ
v2=2(gsinθ)(hsinθ)
- Simplifying this gives:
v2=2gh
- Therefore, the velocity acquired by the particle sliding down the incline is:
v2=√2gh
s=ut+12at2
- Here, s=L, u=0, and a=gsinθ:
L=0⋅t+12(gsinθ)t2
- This simplifies to:
L=12gsinθ⋅t2
hsinθ=12gsinθ⋅t2
t2=2hgsin2θ
t=√2hgsin2θ
t=√2hgsin2θ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.117videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
In the case of a body sliding down a rough inclined plane show that μs=tanθ
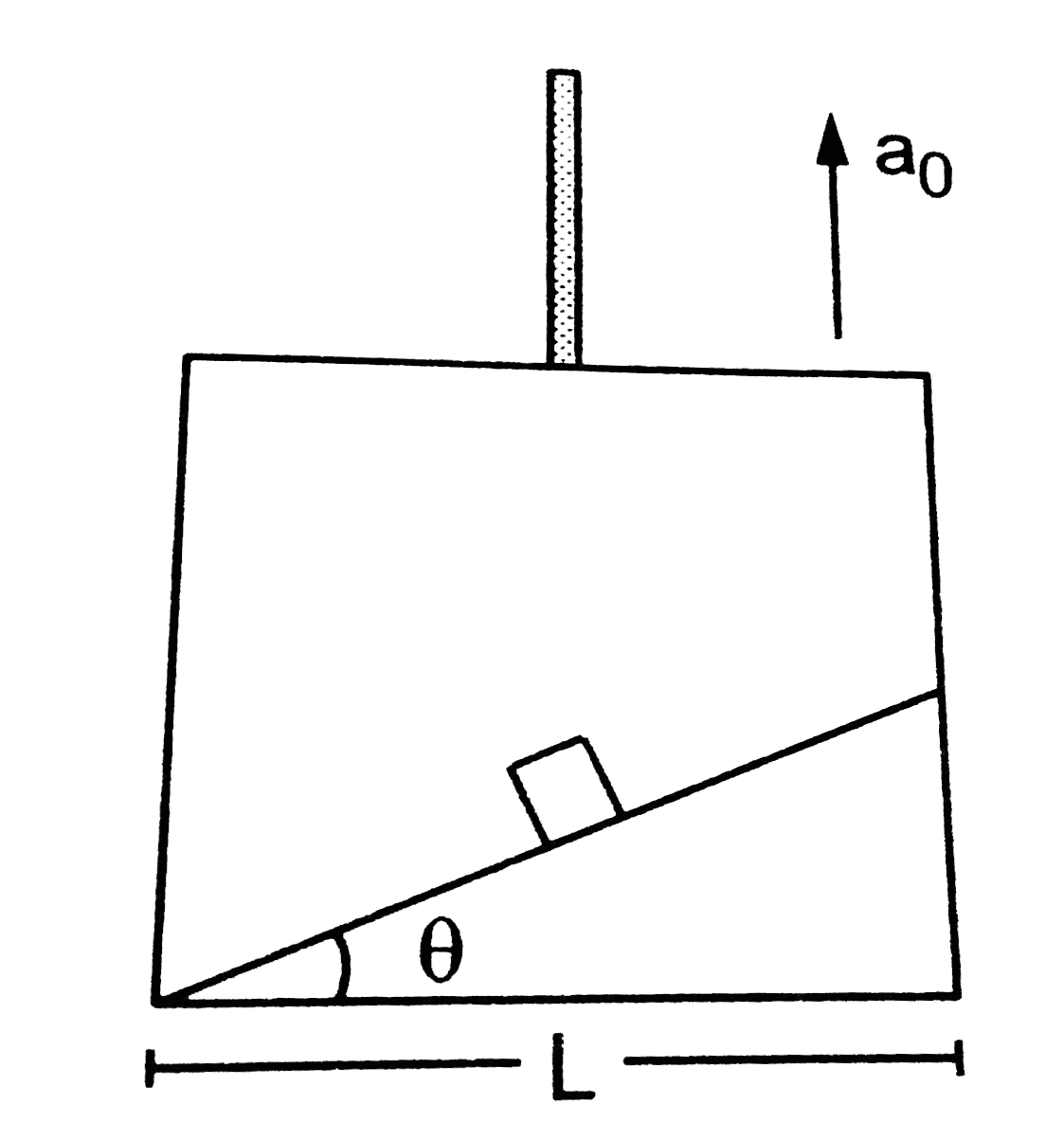
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of the incline has a length L. Find the time taken by the particle to reach the bottom.
 View Solution
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.
 View Solution
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
View SolutionA block slides down a smooth inclined placne when released from the top, while another falls freely from the same point. Which of the following is/are correct ?
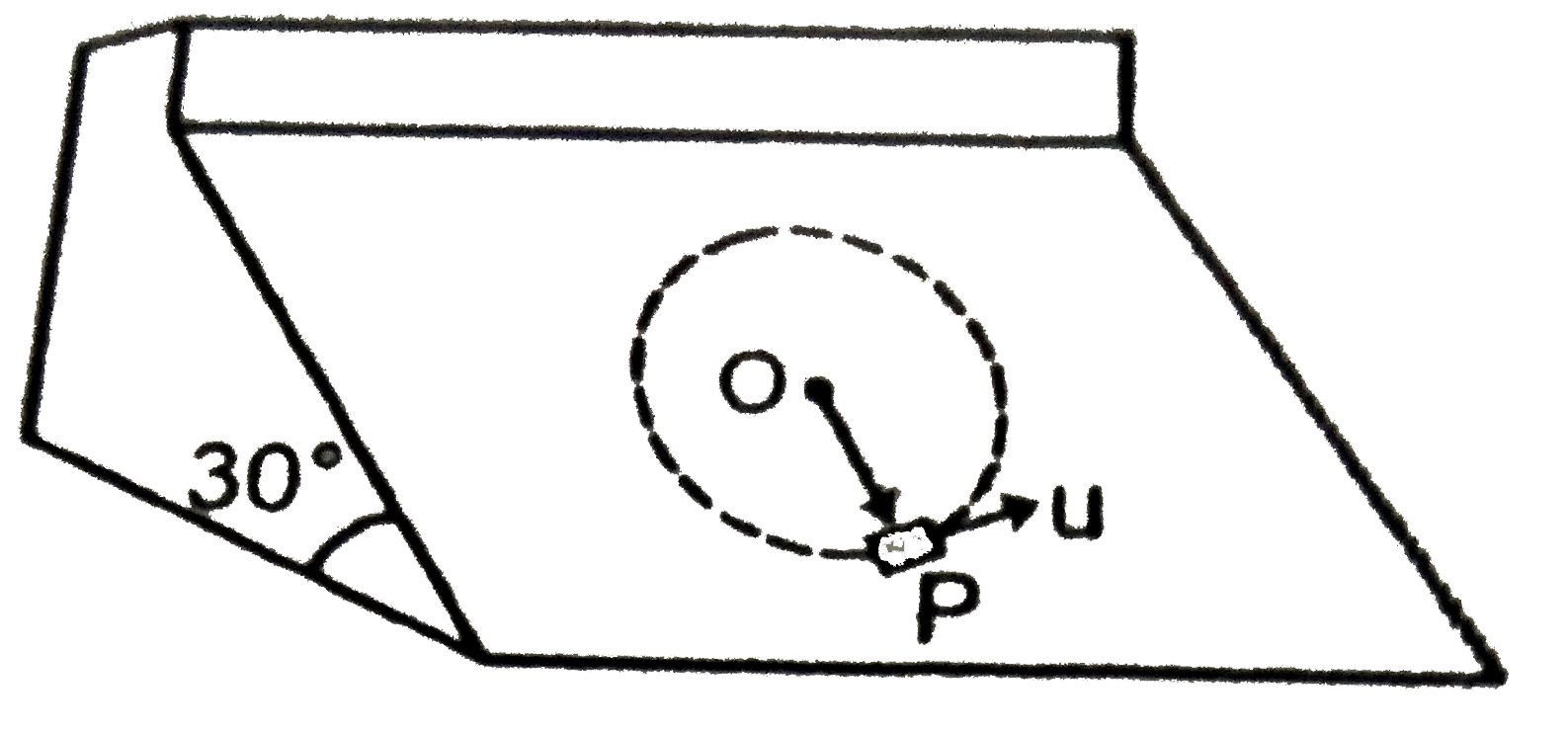
View SolutionA particle is attached with a string of length l which is fixed at point O on an inclined plane what minimum velocity should be given to the particle along the incline so that it may complete a circle on inclined plane ( plane is smooth and initially particle was resting on the inclined plane . )
 View Solution
View SolutionStarting from rest a body slides down a 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
View SolutionA particle starts sliding down a frictionless inclined plane. If Sn is the distance travelled by it from time t=n−1sec, to t=nsec, the ratio Snsn+1 is
View SolutionA particle starts sliding down a frictionless inclined plane. If Sn is the distance travelled by it from time t=n−1sec, to t=nsec, the ratio Snsn+1 is
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
View Solution

