A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
YAx22L
YAx2L2
YAx2L
YAx2L
The correct Answer is:A
To find the work done in stretching a wire of length L and cross-sectional area A made of a material with Young's modulus Y by an amount x, we can follow these steps:
Step 1: Understand Young's Modulus
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=F/AΔL/L
Where:
- F is the force applied,
- A is the cross-sectional area,
- ΔL is the change in length (which is x),
- L is the original length of the wire.
Step 2: Rearranging Young's Modulus
From the definition of Young's modulus, we can rearrange the equation to find the force F:
F=Y⋅A⋅xL
Step 3: Work Done in Stretching the Wire
The work done W in stretching the wire through a distance x can be expressed as:
dW=F⋅dx
Substituting the expression for F:
dW=(Y⋅A⋅xL)dx
Step 4: Integrating to Find Total Work Done
To find the total work done in stretching the wire from 0 to x, we need to integrate dW:
W=∫x0Y⋅A⋅xLdx
Since Y, A, and L are constants, we can take them out of the integral:
W=Y⋅AL∫x0xdx
Step 5: Evaluating the Integral
The integral of x is:
∫xdx=x22
Evaluating this from 0 to x:
W=Y⋅AL⋅(x22−0)=Y⋅AL⋅x22
Step 6: Final Expression for Work Done
Thus, the total work done in stretching the wire by an amount x is:
W=YAx22L
Summary
The work done in stretching the wire is given by:
W=YAx22L
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=F/AΔL/L
Where:
- F is the force applied,
- A is the cross-sectional area,
- ΔL is the change in length (which is x),
- L is the original length of the wire.
From the definition of Young's modulus, we can rearrange the equation to find the force F:
F=Y⋅A⋅xL
The work done W in stretching the wire through a distance x can be expressed as:
dW=F⋅dx
Substituting the expression for F:
dW=(Y⋅A⋅xL)dx
To find the total work done in stretching the wire from 0 to x, we need to integrate dW:
W=∫x0Y⋅A⋅xLdx
Since Y, A, and L are constants, we can take them out of the integral:
W=Y⋅AL∫x0xdx
The integral of x is:
∫xdx=x22
Evaluating this from 0 to x:
W=Y⋅AL⋅(x22−0)=Y⋅AL⋅x22
Thus, the total work done in stretching the wire by an amount x is:
W=YAx22L
The work done in stretching the wire is given by:
W=YAx22L
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (SURFACE TENSION )
Explore 23 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (CALORIMETRY, CHANGE OF STATE & KINETIC THEORY OF GASES )
Explore 30 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:GRAVITATION
Explore 25 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
A metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionA uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View Solution
Knowledge Check
A steel wire of length 4.5 m and cross-sectional area 3×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4x10−5m2 under a given load. The ratio of the Young's modulus of steel to that of copper is
A1.3B1.5C1.7D1.9
A point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA steel wire of length 4.7m and cross-sectional area 3×10−6m2 stretches by the same amount as a copper wire of length 3.5m and cross-sectional area of 4×10−6m2 under a given load. The ratio of Young's modulus of steel to that of copper is
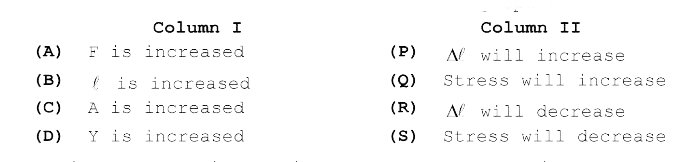
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
View SolutionA wire of length l and cross-sectional are A is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be d and Y?
View SolutionA steel wire of length l and cross sectional area A is stretched by 1 cm under a given load. When the same load is applied to another steel wire of double its length and half of its cross section area, the amount of stretching (extension) is
View SolutionA wire havinga length L and cross- sectional area A is suspended at one of its ends from a ceiling . Density and young's modulus of material of the wire are ρ and Y, respectively. Its strain energy due to its own weight is ρ2g2AL3αY. Find the vqalue of α
View SolutionA metal wire of length L, area of cross-section A and young's modulus Y is stretched by a variable force F such that F is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is l
View Solution
