A point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
12π√LAmY
12π√LAmY
12π√YAmL
12π√mYAL
The correct Answer is:C
To find the frequency of oscillation for a point mass m suspended at the end of a massless wire of length l and cross-sectional area A, with Young's modulus Y, we can follow these steps:
Step 1: Understand the System
We have a mass m hanging from a wire. When the mass is displaced from its equilibrium position and released, it will undergo simple harmonic motion (SHM).
Step 2: Apply Young's Modulus
Young's modulus Y relates stress and strain in the wire. The formula for Young's modulus is given by:
Y=StressStrain=F/AΔl/l
Where:
- F is the force applied (weight of the mass, mg)
- A is the cross-sectional area of the wire
- Δl is the change in length of the wire
- l is the original length of the wire
Rearranging this gives us:
F=Y⋅A⋅Δll
Step 3: Relate Force to Displacement
In SHM, the restoring force F can also be expressed as:
F=−kΔx
Where k is the spring constant and Δx is the displacement from the equilibrium position. By comparing both expressions for force, we can equate them:
mg=Y⋅A⋅Δll
Step 4: Identify the Spring Constant
From the expression F=Y⋅A⋅Δll, we can identify the spring constant k:
k=Y⋅Al
Step 5: Determine the Frequency of Oscillation
The frequency f of oscillation for a mass-spring system is given by:
f=12π√km
Substituting the expression for k:
f=12π√Y⋅A/lm
Final Expression
Thus, the frequency of oscillation is:
f=12π√Y⋅Am⋅l
Summary
The frequency of oscillation for the simple harmonic motion of the mass suspended from the wire is:
f=12π√Y⋅Am⋅l
We have a mass m hanging from a wire. When the mass is displaced from its equilibrium position and released, it will undergo simple harmonic motion (SHM).
Young's modulus Y relates stress and strain in the wire. The formula for Young's modulus is given by:
- F is the force applied (weight of the mass, mg)
- A is the cross-sectional area of the wire
- Δl is the change in length of the wire
- l is the original length of the wire
In SHM, the restoring force F can also be expressed as:
From the expression F=Y⋅A⋅Δll, we can identify the spring constant k:
The frequency f of oscillation for a mass-spring system is given by:
Thus, the frequency of oscillation is:
The frequency of oscillation for the simple harmonic motion of the mass suspended from the wire is:
Similar Questions
An object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View Solution
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2LA metal wire of length L1 and area of cross section A is attached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
A[(Y1Y2)A][2(Y1L2+Y2L1)]B[(Y1Y2)A](L1L2)2C[(Y1Y2)A](Y1L2+Y2L1)D[(Y1Y2)1/2A](L2+L1)1/2
A block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionSpeed of transverse wave on a straight wire (mass m, length l , area of cross-section A) is. If the young’s modulus of wire is Y, the extension of wire over its natural length, is independent of
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
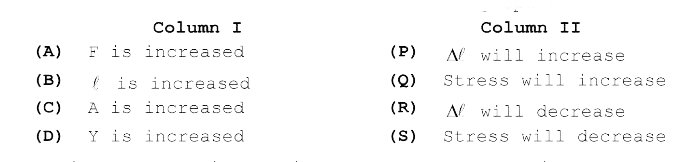
View SolutionIf two wires of same length l and are of the cross-section A with young modulus Y and 2Y connect in series and one end is fixed on roof and another end with mass m makes simple harmonic motion, then the time period is
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View Solution
