The work done is increasing the size of a soap film from 10 cm × 6 cm to 10 cm × 11 cm is 3×10−4 joule. The surface tension of the film is
1.5×10−2 N/m
3.0×10−2 N/m
6.0×10−2 N/m
11.0×10−2 N/m
The correct Answer is:A
To solve the problem, we need to find the surface tension of the soap film given the work done in increasing its size. Here's a step-by-step solution:
Step 1: Understand the given data
- Initial dimensions of the soap film: 10 cm x 6 cm
- Final dimensions of the soap film: 10 cm x 11 cm
- Work done (W) to increase the size: 3×10−4 Joules
Step 2: Convert dimensions to meters
- Initial dimensions in meters:
- Width = 10 cm = 0.1 m
- Height = 6 cm = 0.06 m
- Final dimensions in meters:
- Width = 10 cm = 0.1 m
- Height = 11 cm = 0.11 m
Step 3: Calculate the initial and final areas
- Initial area (A_initial):
Ainitial=Width×Height=0.1m×0.06m=0.006m2
- Final area (A_final):
Afinal=Width×Height=0.1m×0.11m=0.011m2
Step 4: Calculate the change in area (ΔA)
- Change in area (ΔA):
ΔA=Afinal−Ainitial=0.011m2−0.006m2=0.005m2
Step 5: Account for the surface tension acting on both sides of the film
Since the surface tension acts on both sides of the film, the effective change in area for the calculation of work done will be:
ΔAeffective=2×ΔA=2×0.005m2=0.01m2
Step 6: Use the work done formula to find surface tension (T)
The work done (W) is related to surface tension (T) and the change in area (ΔA) by the formula:
W=T×ΔAeffective
Rearranging to find surface tension:
T=WΔAeffective
Substituting the values:
T=3×10−4J0.01m2=3×10−2N/m
Final Answer
The surface tension of the soap film is 3×10−2N/m.
---
- Initial dimensions of the soap film: 10 cm x 6 cm
- Final dimensions of the soap film: 10 cm x 11 cm
- Work done (W) to increase the size: 3×10−4 Joules
- Initial dimensions in meters:
- Width = 10 cm = 0.1 m
- Height = 6 cm = 0.06 m
- Final dimensions in meters:
- Width = 10 cm = 0.1 m
- Height = 11 cm = 0.11 m
- Initial area (A_initial):
Ainitial=Width×Height=0.1m×0.06m=0.006m2
- Final area (A_final):
Afinal=Width×Height=0.1m×0.11m=0.011m2
- Change in area (ΔA):
ΔA=Afinal−Ainitial=0.011m2−0.006m2=0.005m2
Since the surface tension acts on both sides of the film, the effective change in area for the calculation of work done will be:
ΔAeffective=2×ΔA=2×0.005m2=0.01m2
The work done (W) is related to surface tension (T) and the change in area (ΔA) by the formula:
W=T×ΔAeffective
Rearranging to find surface tension:
T=WΔAeffective
Substituting the values:
T=3×10−4J0.01m2=3×10−2N/m
The surface tension of the soap film is 3×10−2N/m.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (CALORIMETRY, CHANGE OF STATE & KINETIC THEORY OF GASES )
30 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - INTERNAL ENERGY
40 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (ELASTICITY )
22 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
Knowledge Check
The work done in increasing the size of a rectangular soap film with dimensions 8 cm x 3.75 cm to 10 cm x 6 cm is 2×10−4J. The surface tension of the film in (Nm−1) is
A1.65×10−2B3.3×10−2C6.6×10−2D8.25×10−2
A rectangular film of liquid is extended from (4cm×2cm) to (5cm×4×cm). If the work done is 3×10−4J, the value of the surface tension of the liquid is
View SolutionWork done in increasing the size of a soap bubble from a radius of 3cm to 5cm is nearly (Surface tension of soap solution =0.03Nm−1)
View SolutionIf 72×10−5 J of work is done to increase the radius of a soap bubble from 2 cm to 3 cm. What is the surface tension of the soap solution?
View SolutionHow much work will be done in increasing the diameter of a soap bubble from 2cm to 5cm? Surface tension solution is 3.0×10−2N/m.
View SolutionHow much work will be done in increasing the diameter of a soap bubble from 2 cm to 5 cm. Surface tension of soap solution is 3.0×10−2Nm−1.
View SolutionCalculate the work down against surface tension in blowing a soap bubble from a radius of 10cm to 20cm, if the surface tension of soap solution in 25×10−3N/m.
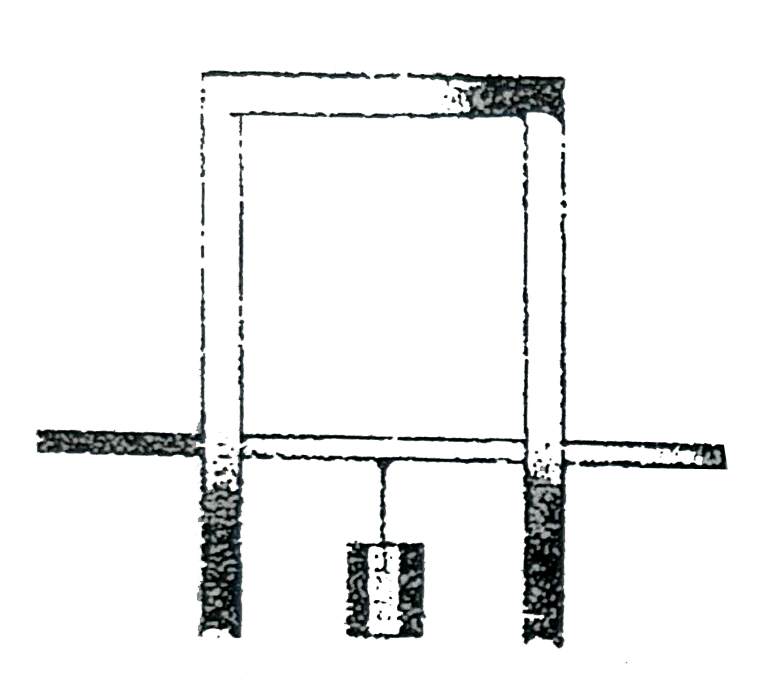
View SolutionA rectagular wire frame with one movable side is convered by a soap film (fig.). What force should be applied to the movable side to counterbalance it ? What work will be done if this side of the frame is moved a distance S=2cm ? The length of the movable side is l=6cm. The surface tension of the soap film is α=40dyne/cm.
View Solution
