The radii of two soap bubbles are . They meet to produce a double bubble. The radius of their common interface is
The correct Answer is:C
To find the radius of the common interface of two soap bubbles with radii r1 and r2 (where r2<r1), we can follow these steps:
Step 1: Understand the Pressure Difference in Soap Bubbles
The excess pressure inside a soap bubble is given by the formula:
ΔP=Pinside−Poutside=4TR
where T is the surface tension of the soap solution and R is the radius of the bubble.
Step 2: Set Up the Equations for Each Bubble
For bubble 1 with radius r1:
P1−P0=4Tr1(1)
For bubble 2 with radius r2:
P2−P0=4Tr2(2)
Here, P0 is the external pressure.
Step 3: Set Up the Equation for the Common Interface
For the common interface of the double bubble, the excess pressure difference is:
P2−P1=4Tr
where r is the radius of the common interface.
Step 4: Substitute the Pressures from Equations (1) and (2)
Substituting P1 and P2 from equations (1) and (2):
(P0+4Tr2)−(P0+4Tr1)=4Tr
This simplifies to:
4Tr2−4Tr1=4Tr
Step 5: Simplify the Equation
Dividing through by 4T (assuming T≠0):
1r2−1r1=1r
Step 6: Rearranging the Equation
Rearranging gives us:
1r=1r1−1r2
Step 7: Finding the Radius of the Common Interface
Taking the reciprocal of both sides, we find:
r=r1r2r1−r2
Final Answer
Thus, the radius of the common interface of the double bubble is:
r=r1r2r1−r2
---
The excess pressure inside a soap bubble is given by the formula:
ΔP=Pinside−Poutside=4TR
where T is the surface tension of the soap solution and R is the radius of the bubble.
For bubble 1 with radius r1:
P1−P0=4Tr1(1)
For bubble 2 with radius r2:
P2−P0=4Tr2(2)
Here, P0 is the external pressure.
For the common interface of the double bubble, the excess pressure difference is:
P2−P1=4Tr
where r is the radius of the common interface.
Substituting P1 and P2 from equations (1) and (2):
(P0+4Tr2)−(P0+4Tr1)=4Tr
This simplifies to:
4Tr2−4Tr1=4Tr
Dividing through by 4T (assuming T≠0):
1r2−1r1=1r
Rearranging gives us:
1r=1r1−1r2
Taking the reciprocal of both sides, we find:
r=r1r2r1−r2
Thus, the radius of the common interface of the double bubble is:
r=r1r2r1−r2
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (CALORIMETRY, CHANGE OF STATE & KINETIC THEORY OF GASES )
Explore 30 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:INTERNAL ENERGY
Explore 40 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (ELASTICITY )
Explore 22 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
The radii of two soap bubbles are ri and r2. In isothermal conditions, two meet together in vacuum. Then the radius kof the resultant bubble is given by
View SolutionUnder isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View Solution
Knowledge Check
Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
Abubbles A and B will be equalBbubbles A will be less than that in bubbles BCbubbles A will be greater than that in bubble BDbubbles A and B will be zero.The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2
Two soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View SolutionThe excess pressure inside a soap bubble of radius R is (S is the surface tension)
View SolutionA soap bubble of radius r is placed on another bubble of radius 2r. The radius of the surface common to both the bubbles is
View SolutionTwo soap bubbles are stuck together with an intermediate film separating them. Compute the radius of curvature of this film given that the radii of the bubbles in this arrangement are r1 and r2 respectively. If r1>r2 state clearly which way the intermediate film will bulge.
For the case when r1=r2=2cm calculate he radius of the bubble formed by bursting the intermediate film. The volume of a spherical dome of radius R and height h is πb2(3R−b)/3.
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View SolutionTwo soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
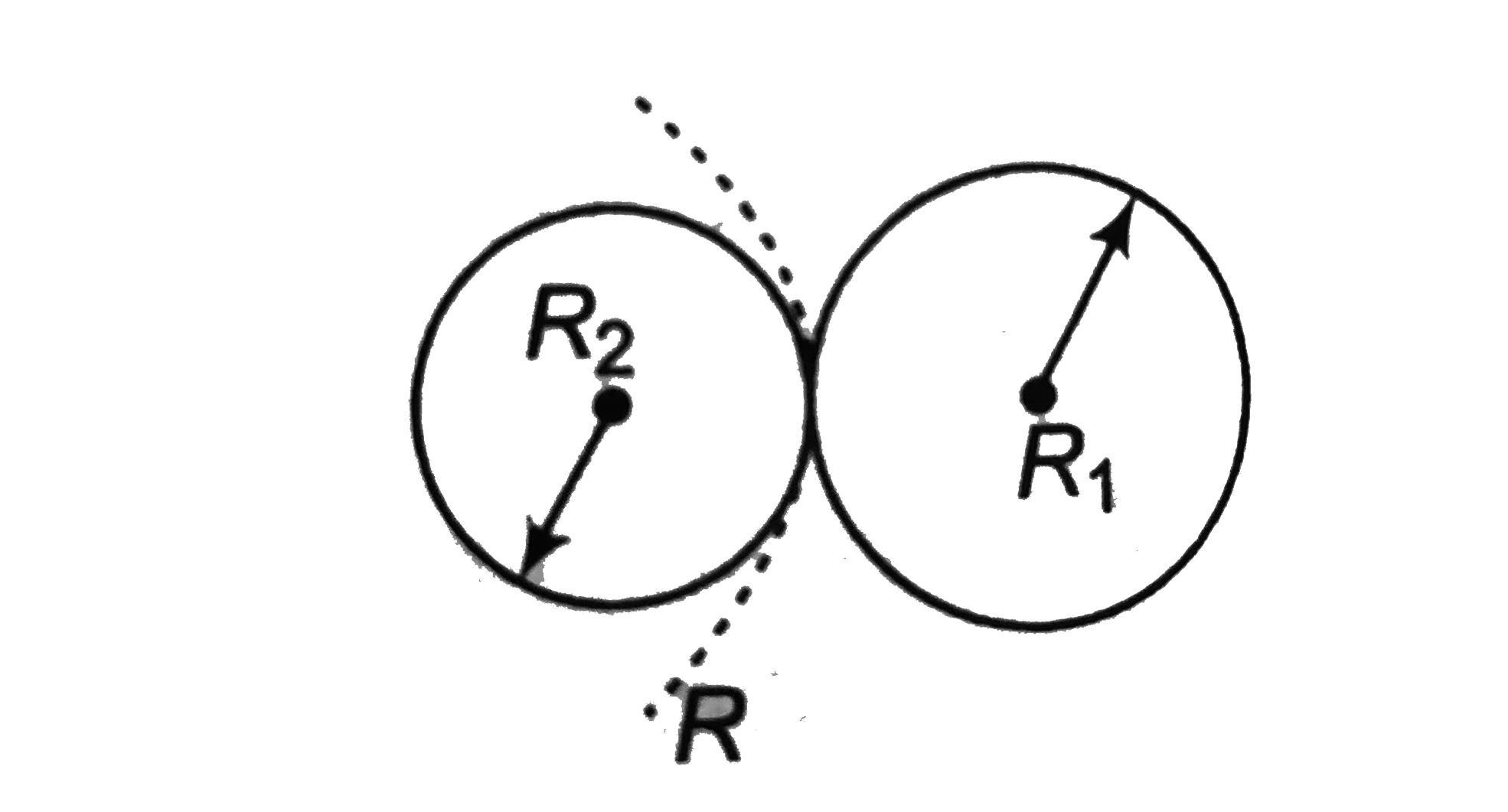 .
.
View Solution