Match list (Physical Quantity ) with List II (Dimensions) and select the correct answer using the codes givn below the list
The correct Answer is:B
To solve the problem of matching physical quantities with their corresponding dimensions, we will analyze each item in List I and determine its dimensional formula.
1. Relative Density (A):
- Relative density is defined as the ratio of the density of a substance to the density of water.
- Since both densities have the same units (mass per unit volume), the units cancel out.
- Therefore, relative density is a dimensionless quantity.
- Dimensional Formula: M0L0T0 (which corresponds to option 3).
2. Potential Energy (B):
- Potential energy (PE) is given by the formula PE=mgh, where m is mass, g is acceleration due to gravity, and h is height.
- The dimensions of mass m are M, height h has dimensions L, and g can be expressed as LT−2.
- Therefore, the dimensional formula for potential energy is:
(PE)=M⋅(LT−2)⋅L=ML2T−2
- Dimensional Formula: ML2T−2 (which corresponds to option 5).
3. Viscosity (C):
- Viscosity is defined as the resistance of a fluid to flow and is given by the formula:
Viscosity=ForceArea⋅Velocity=FA⋅v
- The dimensions of force F are MLT−2, area A is L2, and velocity v is LT−1.
- Therefore, the dimensional formula for viscosity is:
(Viscosity)=MLT−2L2⋅(LT−1)=MLT−2L3T−1=ML−1T−1
- Dimensional Formula: ML−1T−1 (which corresponds to option 4).
4. Linear Momentum (D):
- Linear momentum p is defined as the product of mass and velocity:
p=mv
- The dimensions of mass m are M and velocity v is LT−1.
- Therefore, the dimensional formula for linear momentum is:
(p)=M⋅(LT−1)=MLT−1
- Dimensional Formula: MLT−1 (which corresponds to option 2).
Summary of Matches:
- (A) Relative Density → (3) M0L0T0
- (B) Potential Energy → (5) ML2T−2
- (C) Viscosity → (4) ML−1T−1
- (D) Linear Momentum → (2) MLT−1
Final Answer:
The correct matching is:
- A - 3
- B - 5
- C - 4
- D - 2
- Relative density is defined as the ratio of the density of a substance to the density of water.
- Since both densities have the same units (mass per unit volume), the units cancel out.
- Therefore, relative density is a dimensionless quantity.
- Dimensional Formula: M0L0T0 (which corresponds to option 3).
- Potential energy (PE) is given by the formula PE=mgh, where m is mass, g is acceleration due to gravity, and h is height.
- The dimensions of mass m are M, height h has dimensions L, and g can be expressed as LT−2.
- Therefore, the dimensional formula for potential energy is:
(PE)=M⋅(LT−2)⋅L=ML2T−2
- Dimensional Formula: ML2T−2 (which corresponds to option 5).
- Viscosity is defined as the resistance of a fluid to flow and is given by the formula:
Viscosity=ForceArea⋅Velocity=FA⋅v
- The dimensions of force F are MLT−2, area A is L2, and velocity v is LT−1.
- Therefore, the dimensional formula for viscosity is:
(Viscosity)=MLT−2L2⋅(LT−1)=MLT−2L3T−1=ML−1T−1
- Dimensional Formula: ML−1T−1 (which corresponds to option 4).
- Linear momentum p is defined as the product of mass and velocity:
p=mv
- The dimensions of mass m are M and velocity v is LT−1.
- Therefore, the dimensional formula for linear momentum is:
(p)=M⋅(LT−1)=MLT−1
- Dimensional Formula: MLT−1 (which corresponds to option 2).
- (A) Relative Density → (3) M0L0T0
- (B) Potential Energy → (5) ML2T−2
- (C) Viscosity → (4) ML−1T−1
- (D) Linear Momentum → (2) MLT−1
The correct matching is:
- A - 3
- B - 5
- C - 4
- D - 2
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - WAVES
98 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
Knowledge Check
Match List I with List II and select the correct answer by using the codes given below the lists :
 AI-B,II-A,III-C,IV-DBI-A,II-D,III-B,IV-CCI-A,II-D,III-B,IV-CDI-D,II-A,III-B,IV-C
AI-B,II-A,III-C,IV-DBI-A,II-D,III-B,IV-CCI-A,II-D,III-B,IV-CDI-D,II-A,III-B,IV-CMatch List I with List II and select the correct answer by using the codes given below the lists :
 AI-B,II-A,III-C,IV-DBI-A,II-D,III-C,IV-BCI-A,II-D,III-B,IV-CDI-D,II-A,III-B,IV-C
AI-B,II-A,III-C,IV-DBI-A,II-D,III-C,IV-BCI-A,II-D,III-B,IV-CDI-D,II-A,III-B,IV-C
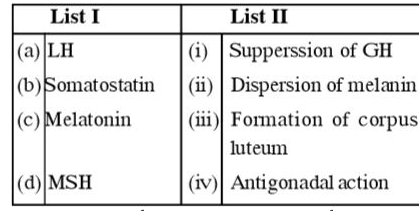
Match list I with list II and select the correct answer using the codes given below the list
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists:

View SolutionMatch List I with List II and select the correct answer using the codes given below the lists:

View SolutionMatch List-I with List-II and select the correct answer using the codes given below the lists

View SolutionMatch List -I with List -II and select the correct answer using the codes given below the lists

View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View Solution


