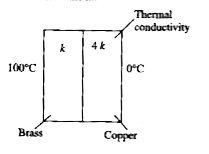
The slab shown in the figure consists of two parallel layers of cooper anb brass of same thickness and having thermal conductivites in the ratio 4:1. IF the free face of the brass is at 100∘C and that of copper is at 0∘C, then the temperature of the interface will be
20∘C
30∘C
40∘C
25∘C
The correct Answer is:A
Step by step video, text & image solution for The slab shown in the figure consists of two parallel layers of cooper anb brass of same thickness and having thermal conductivites in the ratio 4 : 1. IF the free face of the brass is at 100^(@)C and that of copper is at 0^(@)C , then the temperature of the interface will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - WAVES
98 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
A slab consists of two parallel layers of copper and brass of the same thichness and having thermal conductivities in the ratio 1:4 If the free face of brass is at 100∘C anf that of copper at 0∘C the temperature of interface is .
View SolutionTwo plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
View Solution
Knowledge Check
Two cylinders P and Q have the same length and diameter and are made of different materials having thermal conductivities in the ratio 2:3. These two cyinders ar combined to make a cylinder. One end of P is kept at 100∘C and another end of Q at 0∘C. THe temperature at the interface of P and Q is
A30∘CB40∘CC50∘CD60∘C
A slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View SolutionTwo walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View SolutionThree rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png)
View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
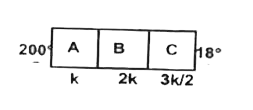
View SolutionA slab consists of two parallel layers of iron and brass 10 cm and 10.9 cm thick and of thermal conductivities 500Wm−1K−1and109Wm−1K−1 respectively. The area of opposite faces are 2m2 each and are at temperatures 373 K and 273 K. Find heat conducted per second across the slab and also the temperature of the interface.
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390Wm−1C−1 and that of steel =46Wm−1C−1 .

View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1.∘C−1 and that of steel =46Wm−1.∘C−1 .

View Solution
