Fig. 144.9 shops to wave pulses travelling along a string in the opposite directions. The velocity of the wave is 3 m/s and the pulses are 9cm apart. Find what has hap-pened to the energy at t=1.5s.
To solve the problem, we need to analyze the wave pulses traveling along a string and determine what happens to the energy at t=1.5 seconds. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the distance traveled by the wave pulses
The distance d traveled by the wave pulses can be calculated using the formula:
d=v×t
where:
- v=3m/s (velocity of the wave)
- t=1.5s
Substituting the values:
d=3m/s×1.5s=4.5m
Step 2: Determine the positions of the wave pulses at t=1.5 seconds
Since the pulses are initially 9cm apart, we need to convert this to meters:
9cm=0.09m
At t=1.5 seconds, each pulse has traveled 4.5m. If we assume one pulse starts at the origin (0 m), the other pulse would start at 0.09m and travel in the opposite direction.
Step 3: Analyze the position of the pulses
At t=1.5 seconds:
- The first pulse (starting from 0 m) will be at 4.5m.
- The second pulse (starting from 0.09m) will be at:
0.09m−4.5m=−4.41m
Step 4: Determine the type of interference
At t=1.5 seconds, the two pulses will overlap. Since they are traveling in opposite directions and are of equal amplitude, they will undergo destructive interference at the point of superposition. This means that the resultant displacement of the string at the center will be zero.
Step 5: Analyze the energy at t=1.5 seconds
Even though the displacement is zero due to destructive interference, the particles of the string still have velocity. The energy in the system is related to the kinetic energy of the particles, which can be expressed as:
Kinetic Energy∝(∂y∂t)2
Step 6: Show that the particle velocity is not zero
To find the particle velocity, we differentiate the displacement equation of the wave:
y=2acos(kx)sin(ωt)
Differentiating with respect to time t:
∂y∂t=2acos(kx)ωcos(ωt)
At t=1.5 seconds, we find that:
- Since sin(ωt)=0, we can find ω such that ω⋅1.5=nπ for integers n.
- For the first harmonic, let’s take n=1, then ω=2π3.
Thus, substituting back:
∂y∂t=2acos(kx)⋅2π3⋅cos(2π3)
Since cos(2π3)=−12, we find that:
∂y∂t≠0
Conclusion
At t=1.5 seconds, the energy has transformed into kinetic energy due to the particle velocities, even though the displacement is zero.
---
The distance d traveled by the wave pulses can be calculated using the formula:
d=v×t
where:
- v=3m/s (velocity of the wave)
- t=1.5s
d=3m/s×1.5s=4.5m
Since the pulses are initially 9cm apart, we need to convert this to meters:
9cm=0.09m
At t=1.5 seconds, each pulse has traveled 4.5m. If we assume one pulse starts at the origin (0 m), the other pulse would start at 0.09m and travel in the opposite direction.
At t=1.5 seconds:
- The first pulse (starting from 0 m) will be at 4.5m.
- The second pulse (starting from 0.09m) will be at:
0.09m−4.5m=−4.41m
At t=1.5 seconds, the two pulses will overlap. Since they are traveling in opposite directions and are of equal amplitude, they will undergo destructive interference at the point of superposition. This means that the resultant displacement of the string at the center will be zero.
Even though the displacement is zero due to destructive interference, the particles of the string still have velocity. The energy in the system is related to the kinetic energy of the particles, which can be expressed as:
Kinetic Energy∝(∂y∂t)2
To find the particle velocity, we differentiate the displacement equation of the wave:
y=2acos(kx)sin(ωt)
Differentiating with respect to time t:
∂y∂t=2acos(kx)ωcos(ωt)
At t=1.5 seconds, we find that:
- Since sin(ωt)=0, we can find ω such that ω⋅1.5=nπ for integers n.
- For the first harmonic, let’s take n=1, then ω=2π3.
∂y∂t=2acos(kx)⋅2π3⋅cos(2π3)
Since cos(2π3)=−12, we find that:
∂y∂t≠0
At t=1.5 seconds, the energy has transformed into kinetic energy due to the particle velocities, even though the displacement is zero.
Topper's Solved these Questions
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Musical Sound
2 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Conceptual Short Answer Questions With Answers
25 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Additional Solved Problems
13 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
A transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10cm/s. The wavelength of the wave is 0.5 m and its amplitude is 10cm. At a particular time t,the snapshot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is

(a) √3π50ˆjm/s
(b)−√3π50ˆjm/s
(c)√3π50ˆim/s
(d) −√3π50ˆim/s
View SolutionA wave pulse on a string on a string has the dimension shown in figure. The wave speed is v=1 cm /s . If point O is a free end. The shape of wave at time t = 3s si

View Solution
Knowledge Check
A wave is represented by the equation
y=Asin(10πx+15πt+π/3)
Where x is in metre and t is in second.
a wave travelling in the positive x-direction with a velocity of 1.5 m/s
a wave travelling in the negative x-direction with a velocity 1.5 m/s
a wave travelling in the negative x-direction with a wavelength of 0.2 m
a wave travelling in the positive x-direction with a wavelength 0.2 mAa wave travelling in the positive x-direction with a velocity of 1.5 m/sBa wave travelling in the negative x-direction with a velocity 1.5 m/sCa wave travelling in the negative x-direction with a wavelength of 0.2 mDa wave travelling in the positive x-direction with a wavelength 0.2 m
Two waves are travelling in same direction along a stretched string. The waves are 90∘ out of phase. Each wave has an amplitude of 4.0 cm. Find the amplitude of the resultant wave.
View SolutionTwo pulses travel in mutually opposite directions in a string with a speed of 2.5cm/s as shown in the figure. Initially the pulses are 10cm apart. What will be the state of the string after two seconds?
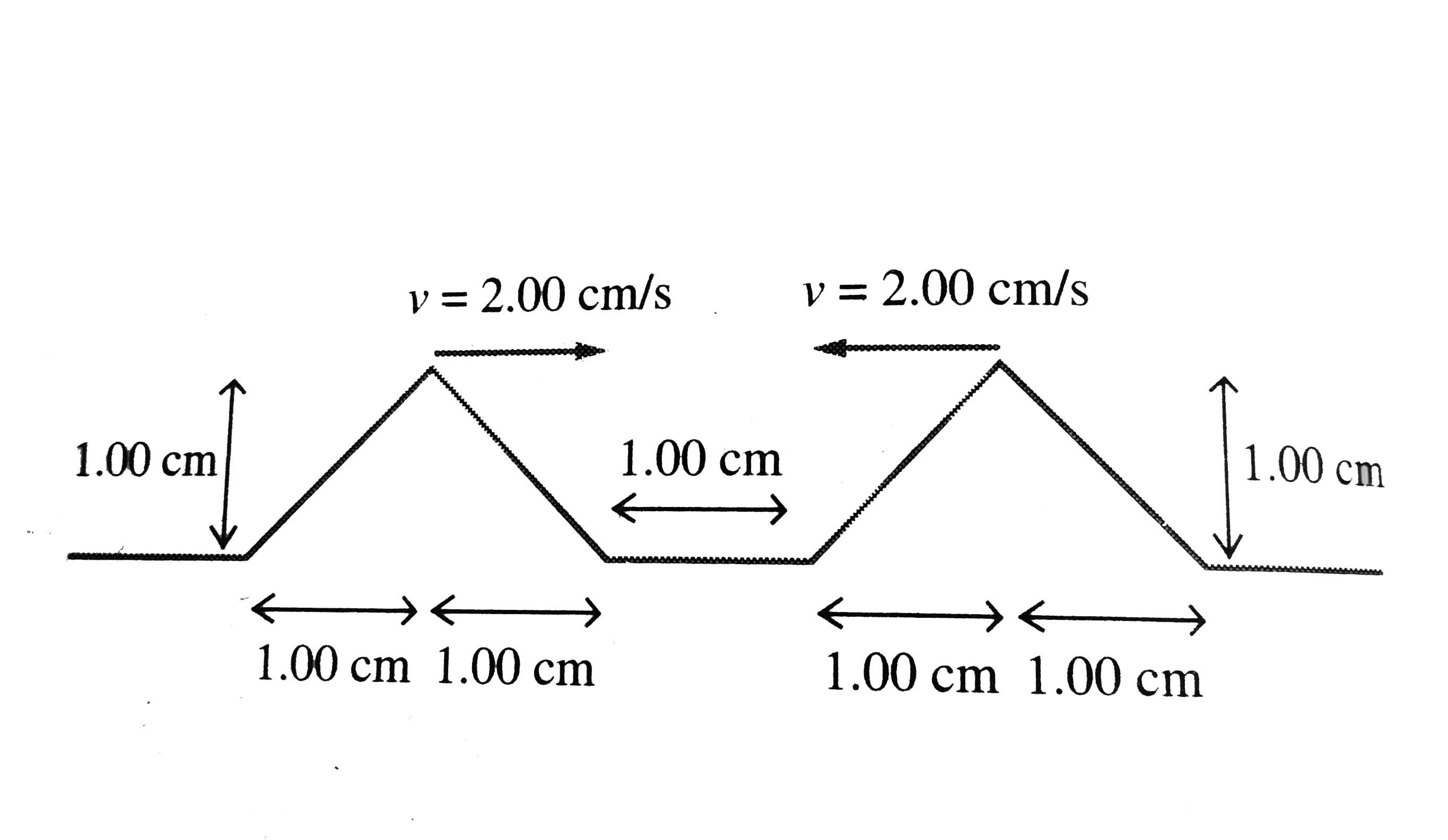
View SolutionTwo triangular wave pulses are travelling toward each other on a stretched string as shown in Fig . 7.25. Both pulses are identical to each other and travels at 2.00cm/s. The leading edges of the pulses are 1.00cmapart at t=0 . Sketch the shape of the string at t=0.250s,t=0.500s,t=0.750s,t=1.000sandt=1.250s.
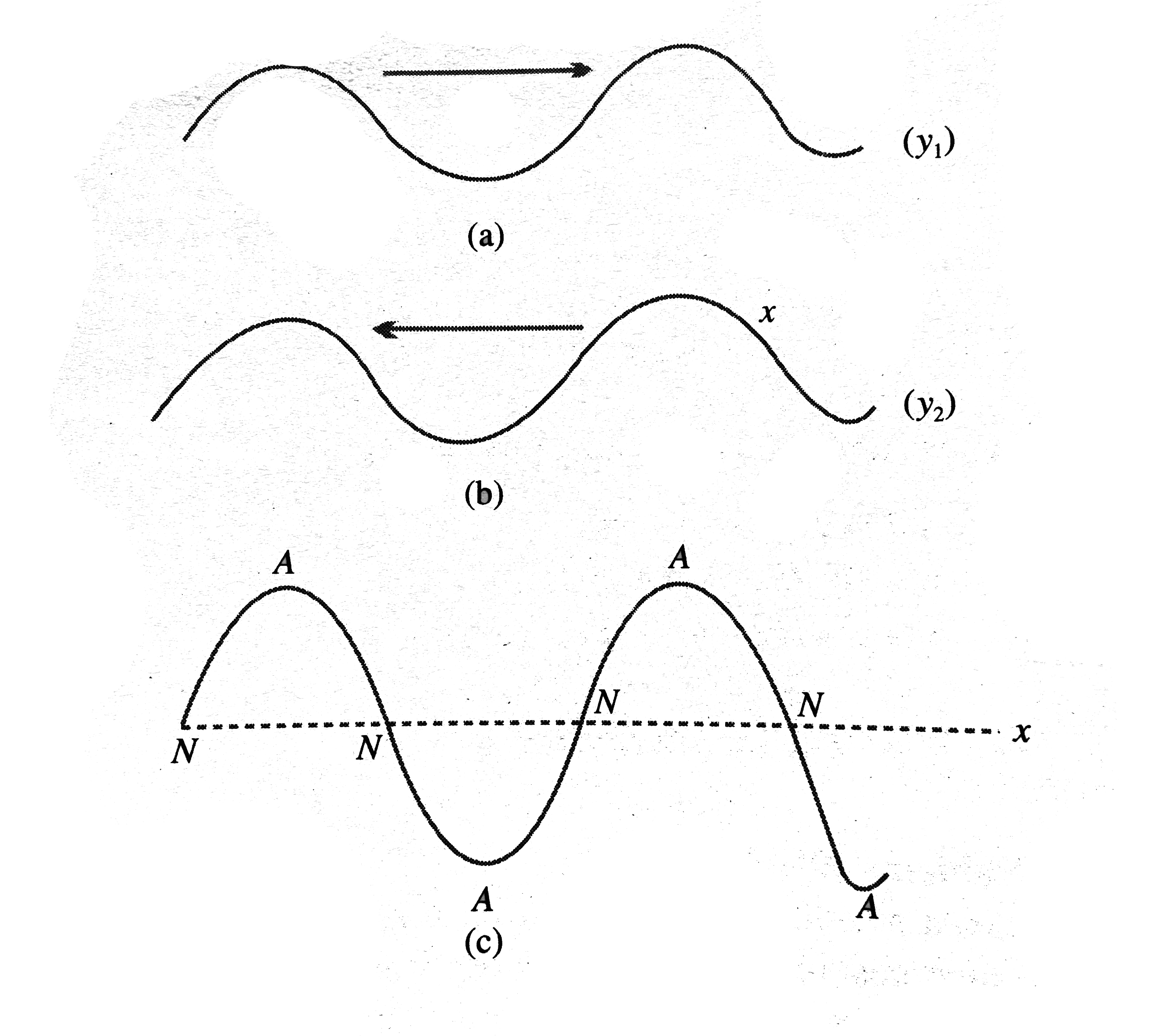
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string named as A
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will be
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described as
View SolutionA standing wave is formed by two harmonic waves, y1=Asin(kx−ωt)andy2=Asin(kx+ωt) travelling on a string in opposite directions. Mass density is 'ρ' and area of cross section is S. Find the total mechanical energy between two adjacent nodes on the string.
View Solution
