Two pulses travel in mutually opposite directions in a string with a speed of 2.5cm/s as shown in the figure. Initially the pulses are 10cm apart. What will be the state of the string after two seconds?




The correct Answer is:C
To solve the problem, we need to determine the position of the two pulses after 2 seconds, given their initial separation and speed.
1. Identify the Given Data:
- Speed of each pulse, v=2.5cm/s
- Initial distance between the two pulses, d=10cm
- Time, t=2s
2. Calculate the Distance Traveled by Each Pulse:
- The distance traveled by each pulse in time t can be calculated using the formula:
Distance=Speed×Time
- For t=2s:
Distance=2.5cm/s×2s=5cm
3. Determine the Final Positions of the Pulses:
- Since the pulses are moving towards each other, each pulse will cover a distance of 5 cm.
- Initially, they are 10 cm apart. After 2 seconds:
- The left pulse moves 5 cm towards the right.
- The right pulse moves 5 cm towards the left.
- Therefore, the new distance between the two pulses will be:
10cm−(5cm+5cm)=0cm
- This means the two pulses will meet and overlap completely.
4. State of the String After 2 Seconds:
- When two identical pulses overlap, they interfere with each other. If they are of the same amplitude and shape, they will cancel each other out at the point of overlap.
- Thus, the resultant amplitude at the point of overlap will be 0, and the string will appear straight at that position.
5. Conclusion:
- After 2 seconds, the state of the string will be such that the two pulses overlap completely, resulting in a straight line with no displacement.
Final Answer:
The state of the string after 2 seconds will be a straight line (resultant amplitude = 0).
---
- Speed of each pulse, v=2.5cm/s
- Initial distance between the two pulses, d=10cm
- Time, t=2s
- The distance traveled by each pulse in time t can be calculated using the formula:
Distance=Speed×Time
- For t=2s:
Distance=2.5cm/s×2s=5cm
- Since the pulses are moving towards each other, each pulse will cover a distance of 5 cm.
- Initially, they are 10 cm apart. After 2 seconds:
- The left pulse moves 5 cm towards the right.
- The right pulse moves 5 cm towards the left.
- Therefore, the new distance between the two pulses will be:
10cm−(5cm+5cm)=0cm
- This means the two pulses will meet and overlap completely.
- When two identical pulses overlap, they interfere with each other. If they are of the same amplitude and shape, they will cancel each other out at the point of overlap.
- Thus, the resultant amplitude at the point of overlap will be 0, and the string will appear straight at that position.
- After 2 seconds, the state of the string will be such that the two pulses overlap completely, resulting in a straight line with no displacement.
The state of the string after 2 seconds will be a straight line (resultant amplitude = 0).
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple Correct Answers Type
5 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Fill in the Blanks Type
34 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Integer
9 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
Two wave pulses travel in opposite directions on a string and approch each other. The shape of the one pulse is same with respect to the other
View SolutionTwo pulses travelling in opposite directions along a string are shown for t=0 in the figure. Plot the shape of the string at t= 1.0, 2.0, 3.0, 4.0 and 5.0s respectively .

View SolutionTwo identical harmonic pulses travelling in opposite directions in a taut string approach each other. At the instant when they completely overlap, the total energy of the string will be
 .
.
View SolutionTwo sinusoidal waves with same wavelengths and amplitudes travel in opposite directions along a string with a speed 10ms−1. If the minimum time interval between two instant when the string is flat is 0.5s, the wavelength of the waves is
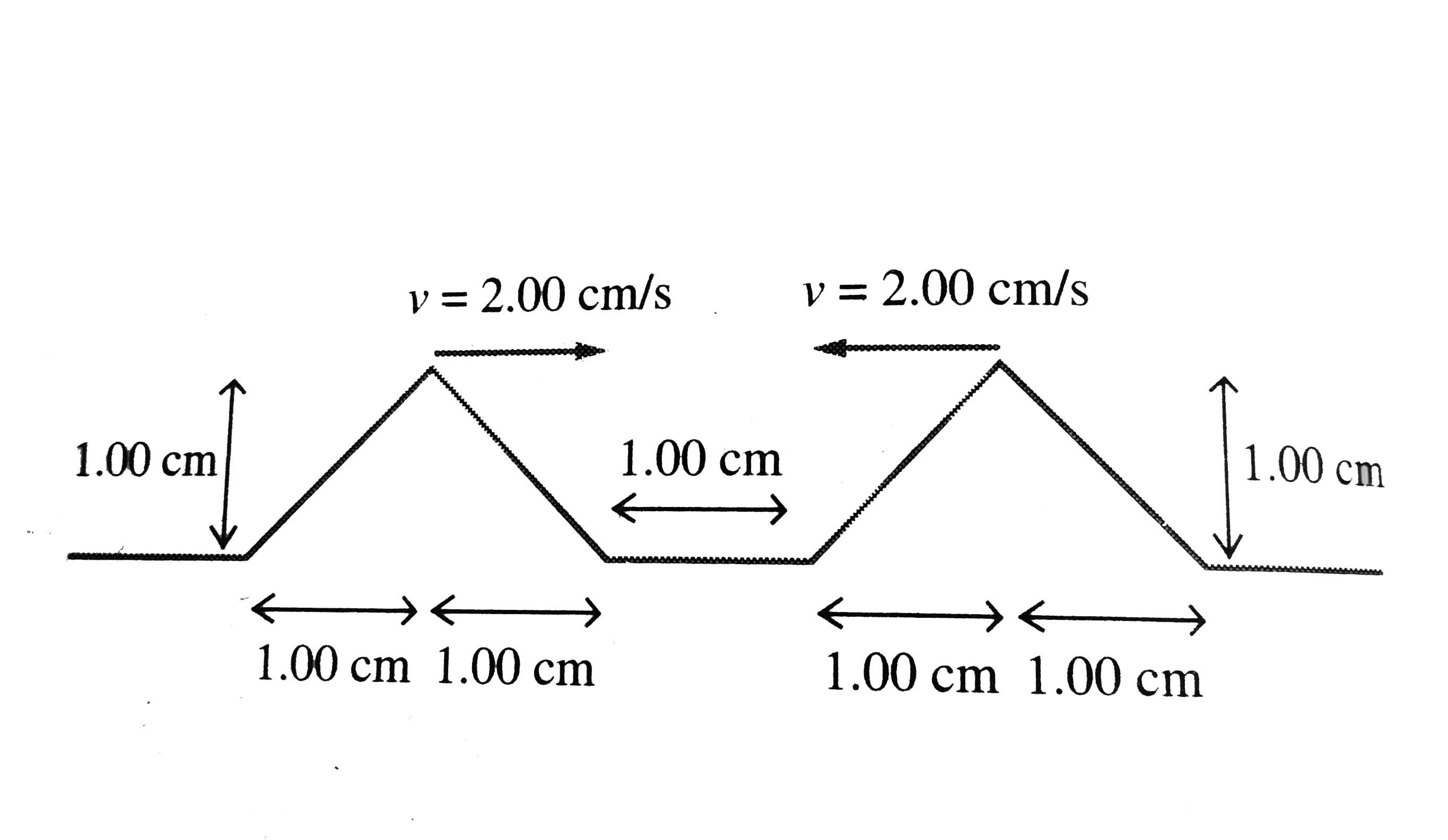
View SolutionTwo triangular wave pulses are travelling toward each other on a stretched string as shown in Fig . 7.25. Both pulses are identical to each other and travels at 2.00cm/s. The leading edges of the pulses are 1.00cmapart at t=0 . Sketch the shape of the string at t=0.250s,t=0.500s,t=0.750s,t=1.000sandt=1.250s.
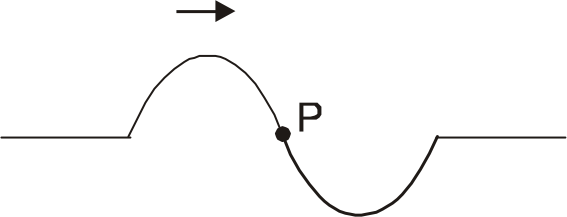
View SolutionA pulse on a string is shown in the figure.P is particle of the string.Then state which of the following are correct .
View SolutionFig. 144.9 shops to wave pulses travelling along a string in the opposite directions. The velocity of the wave is 3 m/s and the pulses are 9cm apart. Find what has hap-pened to the energy at t=1.5s.
View SolutionThe system shown in figure is initially in equilibrium. What is the acceleration of B just after the string connecting B to ground is cut ?

View SolutionA wave pulse is travelling positive x direction with a speed of 4.5 m/s. At time t= 0, the wave pulse is given as y=6x2−3. Here x and y are in metre. Then which function represents the equation of pulse just after 2 second?
View SolutionA pulse shown here is reflected from the rigid wall A and then from free end B. The shape of the string after these 2 reflection will be
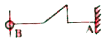
View Solution
