A rod 100 cm in length and of material of density 8×103 kg/m3 is clamped at the centre and attached to a Kundt's tube containing air. The distance between the first and the tenth node when the rod is stroked longitudinally is 135 cm. If the velocity of sound in air is 330 m/s determine the Young's modulus of the material of the rod.
The correct Answer is:3.872×1010N/m2
To determine the Young's modulus of the material of the rod, we can follow these steps:
Step 1: Understand the setup
The rod is clamped at the center, creating nodes at the center and antinodes at the ends. The distance between the first and the tenth node is given as 135 cm.
Step 2: Calculate the wavelength
The distance between nodes in a standing wave is half the wavelength (λ/2). Since the distance between the first and the tenth node is 9 half-wavelengths (from node 1 to node 10), we can express this as:
Distance=9×λ2
Given that this distance is 135 cm (or 1.35 m), we can set up the equation:
1.35=9×λ2
Solving for λ:
λ=1.35×29=0.3m
Step 3: Calculate the frequency
Using the speed of sound in air (v = 330 m/s) and the wavelength (λ = 0.3 m), we can find the frequency (f) using the formula:
v=fλ
Rearranging gives:
f=vλ=3300.3=1100Hz
Step 4: Use the formula for Young's modulus
The formula for Young's modulus (Y) in terms of frequency, density (ρ), and wavelength is:
Y=(2πf)2⋅ρ⋅λ24
Substituting the values:
- f=1100Hz
- ρ=8×103kg/m3
- λ=0.3m
Step 5: Calculate Young's modulus
Substituting into the formula:
Y=(2π×1100)2⋅(8×103)⋅(0.3)24
Calculating (2π×1100)2:
(2π×1100)2≈(6911.5)2≈47851.4(approximately)
Now substituting back:
Y=47851.4⋅8×103⋅0.094
Calculating:
Y=47851.4⋅720004≈34400000004≈860000000N/m2
Thus, the Young's modulus Y≈8.6×108N/m2.
Final Answer
The Young's modulus of the material of the rod is approximately 8.6×108N/m2.
---
The rod is clamped at the center, creating nodes at the center and antinodes at the ends. The distance between the first and the tenth node is given as 135 cm.
The distance between nodes in a standing wave is half the wavelength (λ/2). Since the distance between the first and the tenth node is 9 half-wavelengths (from node 1 to node 10), we can express this as:
Distance=9×λ2
Given that this distance is 135 cm (or 1.35 m), we can set up the equation:
1.35=9×λ2
Solving for λ:
λ=1.35×29=0.3m
Using the speed of sound in air (v = 330 m/s) and the wavelength (λ = 0.3 m), we can find the frequency (f) using the formula:
v=fλ
Rearranging gives:
f=vλ=3300.3=1100Hz
The formula for Young's modulus (Y) in terms of frequency, density (ρ), and wavelength is:
Y=(2πf)2⋅ρ⋅λ24
Substituting the values:
- f=1100Hz
- ρ=8×103kg/m3
- λ=0.3m
Substituting into the formula:
Y=(2π×1100)2⋅(8×103)⋅(0.3)24
Calculating (2π×1100)2:
(2π×1100)2≈(6911.5)2≈47851.4(approximately)
Now substituting back:
Y=47851.4⋅8×103⋅0.094
Calculating:
Y=47851.4⋅720004≈34400000004≈860000000N/m2
Thus, the Young's modulus Y≈8.6×108N/m2.
The Young's modulus of the material of the rod is approximately 8.6×108N/m2.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - WAVESEXERCISE - From Beats15videos
WAVES
- BOOK - ICSECHAPTER - WAVESEXERCISE - From Doppler Effect16videos
WAVES
- BOOK - ICSECHAPTER - WAVESEXERCISE - From Sound Wave Velocity37videos
WAVES
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS79videos
VECTORS SCALARS ELEMENTARY CALCULUS
Similar Questions
Two sounds are heard at the end of an iron rod 5 km long at an interval of 14 seconds, when a source of sound is placed at the other end of the rod. The velocity of sound in air is 330 m/s. the velocity of sound in iron is aproximately
View SolutionSix antinodes are observed in the air column when a standing wave forms in a Kundt's tube . What is the length of the air column if steel bar of 1m length is clamped at the middle .
The velocity of sound in steel is 5250m/s and in air 343m/s.View SolutionWhen a rod of length 2.5 m and radius 10 mm is subjected to a force the elongation is 3mm and decrease of radius is 0.0025 mm. Find poisson.s ratio of the material of the rod.
View SolutionAn open organ pipe of length 11cm in its fundamental mode vibrates in resonance with the first overtone of a closed organ pipe of length 13.2cm filled with some gas . If the velocity of sound in air is 330m/s, calculate the velocity of sound in the unknown gas .
View SolutionA Kundt's tube experiment is conducted with a 1m long glass rod , twice , one with air and the other with hydrogen , gas filled in the tube . In the first case , there were 11 heaps of lycopodium powder within a length of 64.4cm between the first and the last . The corresponding parameters in the second case are 5 nodal heaps within 99.7cm length.
Find the velocity of sound in glass and in hydrogen m if that in air be 335m/s.View SolutionA closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]
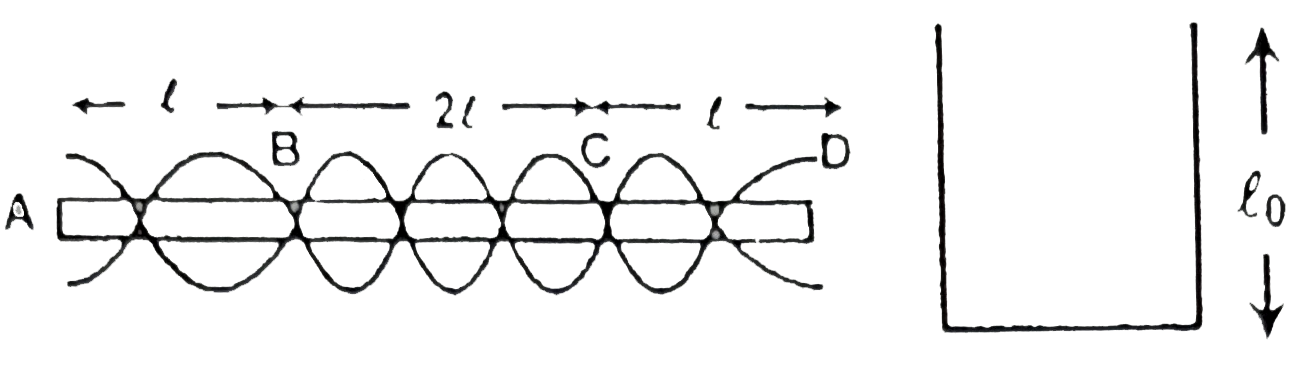 View Solution
View SolutionA closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]
 View Solution
View SolutionWhen air of density 1.3kg/m3 flows across the top of the tube shown in the accompanying figure, water rises in the tube to a height of 1.0cm. What is the speed of air?
 View Solution
View SolutionA rod of 1.5m length and uniform density 104kg/m3 is rotating at an angular velocity 400rad/sec about its one end in a horizontal plane. Find out elongation in rod.
Given y=2×1011N/m2
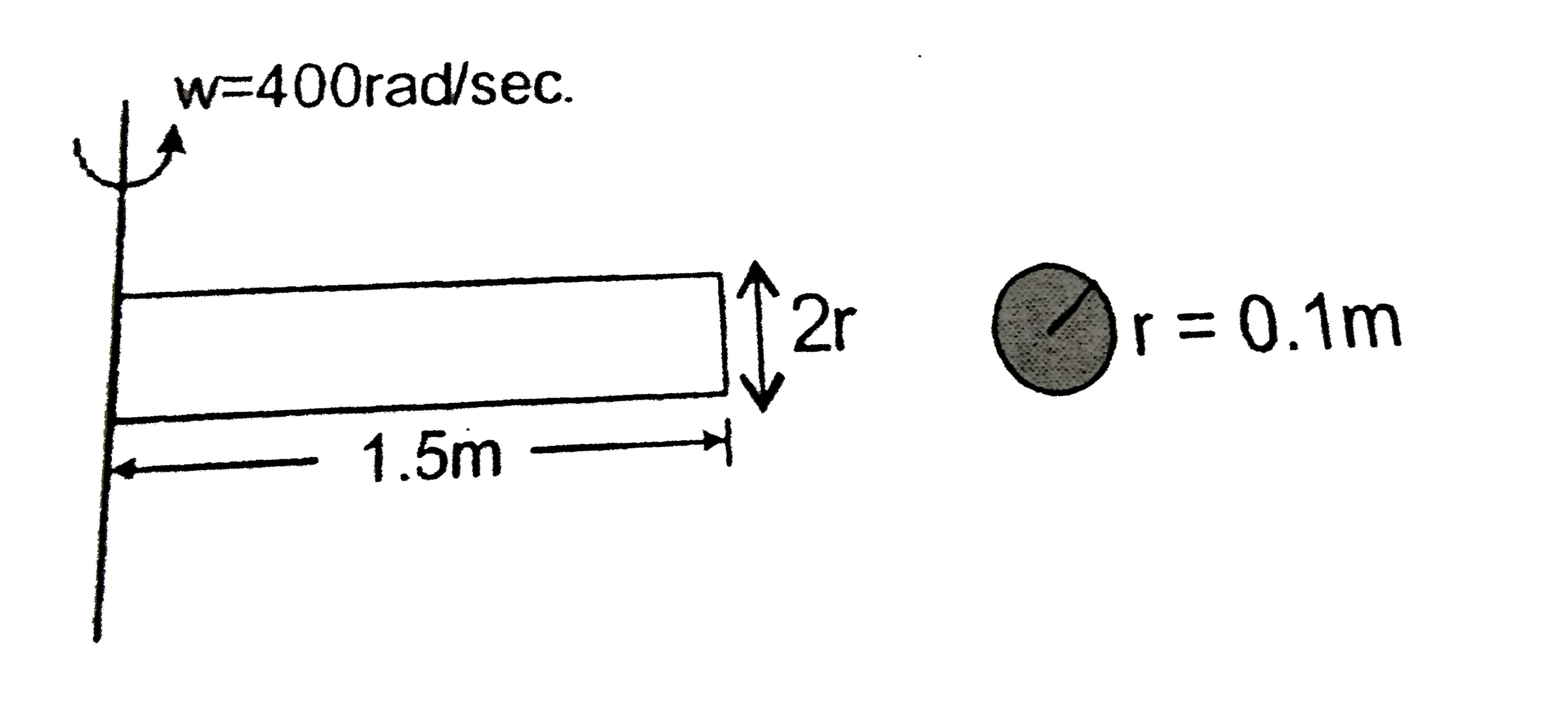 View Solution
View SolutionClamped at the middle a metal rod of length 1m and density 7.5×103kg/m3 gives dust heaps at intervals of 8cm. Calculate the Young's modulus of the material of the rod. Velocity of sound in the gas used in 400m/s.
View Solution

