A plane wave of monochromatic light falls normally on a uniform thin or oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive is observed for λ=5000Å and λ=1000Å and for no other wavelength in between. If μ of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
6.738×10(−5)cm
5.7×10−5cm
4×10−5cm
2.8×10−5cm
The correct Answer is:a
To solve the problem step by step, we will analyze the conditions for destructive interference in a thin film of oil over a glass plate.
Step 1: Understanding the Setup
We have a thin film of oil (refractive index μ=1.3) on a glass plate (refractive index n=1.5). Light is incident normally on the film, and we observe complete destructive interference at two specific wavelengths: λ1=5000Å and λ2=1000Å.
Step 2: Path Difference Condition for Destructive Interference
For destructive interference in a thin film, the condition is given by:
Δx=2μt=(m+12)λ
where m is an integer (0, 1, 2, ...), λ is the wavelength of light, and t is the thickness of the film.
Step 3: Setting Up Equations for Both Wavelengths
For the two wavelengths, we can write:
1. For λ1=5000Å:
2μt=(m1+12)λ1
2. For λ2=1000Å:
2μt=(m2+12)λ2
Step 4: Equating the Two Equations
Since both expressions equal 2μt, we can set them equal to each other:
(m1+12)λ1=(m2+12)λ2
Step 5: Substituting Values
Substituting λ1=5000Å and λ2=1000Å:
(m1+12)⋅5000=(m2+12)⋅1000
Step 6: Rearranging the Equation
Rearranging gives:
5000m1+2500=1000m2+500
5000m1−1000m2=−2000
Step 7: Solving for Integer Values
We can express m2 in terms of m1:
m2=5m1+2
Step 8: Substituting Back to Find Thickness
Now, we can substitute m1 and m2 back into either of the original equations to find t. Using m1=0 (the first order):
2⋅1.3⋅t=(0+12)⋅5000
2.6t=2500
t=25002.6≈961.54Å
Final Answer
The thickness of the oil film is approximately t≈961.54Å.
---
We have a thin film of oil (refractive index μ=1.3) on a glass plate (refractive index n=1.5). Light is incident normally on the film, and we observe complete destructive interference at two specific wavelengths: λ1=5000Å and λ2=1000Å.
For destructive interference in a thin film, the condition is given by:
Δx=2μt=(m+12)λ
where m is an integer (0, 1, 2, ...), λ is the wavelength of light, and t is the thickness of the film.
For the two wavelengths, we can write:
1. For λ1=5000Å:
2μt=(m1+12)λ1
2. For λ2=1000Å:
2μt=(m2+12)λ2
Since both expressions equal 2μt, we can set them equal to each other:
(m1+12)λ1=(m2+12)λ2
Substituting λ1=5000Å and λ2=1000Å:
(m1+12)⋅5000=(m2+12)⋅1000
Rearranging gives:
5000m1+2500=1000m2+500
5000m1−1000m2=−2000
We can express m2 in terms of m1:
m2=5m1+2
Now, we can substitute m1 and m2 back into either of the original equations to find t. Using m1=0 (the first order):
2⋅1.3⋅t=(0+12)⋅5000
2.6t=2500
t=25002.6≈961.54Å
The thickness of the oil film is approximately t≈961.54Å.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
White light reflected at normal incidence from a soap film has minima at 6500Å and maxima at 7500Å in the visible region without minimum in between. If μ is 53 for the thin film, thickness of the film is
View SolutionBlue light of wavelength 480 nm is most strongly reflected off a thin film of oil on a glass slab when viewed near normal incidence. Assuming that the index of refraction of the oil is 1.2 and that of the glass is 1.6, what is the minimum thickness of the oil film (other then zero)?
View SolutionA plane monochromatic light wave falls normally on a diaphragm with two narrow slits separated by 2.5mm. The fringe pattern is formed on a screen 100 cm behind the diaphragm. By what distance will these fringes be displaced, when one of the slits is covered by a glass plate (μ=1.5) of thickness 10μm?
View SolutionWavelength of light in vaccum is 5890 Å, then its wavelength in glass (μ=1.5) will be
View SolutionWhen white light is incident normally an oil film of thickness 10−4cm and refractive index. 1.4 then the wavelength which will not be seen in the reflected system of light is
View SolutionWhen the plastic thin film of refractive index 1.45is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes.The thickness of the film will be ,if the wavelength of light is5890Å
View SolutionWhite light may be considered to be mixture of waves of λ ranging between 3900Å and 7800Å. An oil film of thickness 10,000Å is examined normally by the reflected light. If μ=1.4, then the film appears bright for
View SolutionIn YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
View SolutionIn YDSE, a glass slab of refractive index, μ=1.5 and thickness 'l' is introduced in one of the interfening beams of wavelength λ=5000A. If on introducing the slab, the central fringe shift by 2 mm, then thickness of stab would be (Fringe width, β=0.2mm)
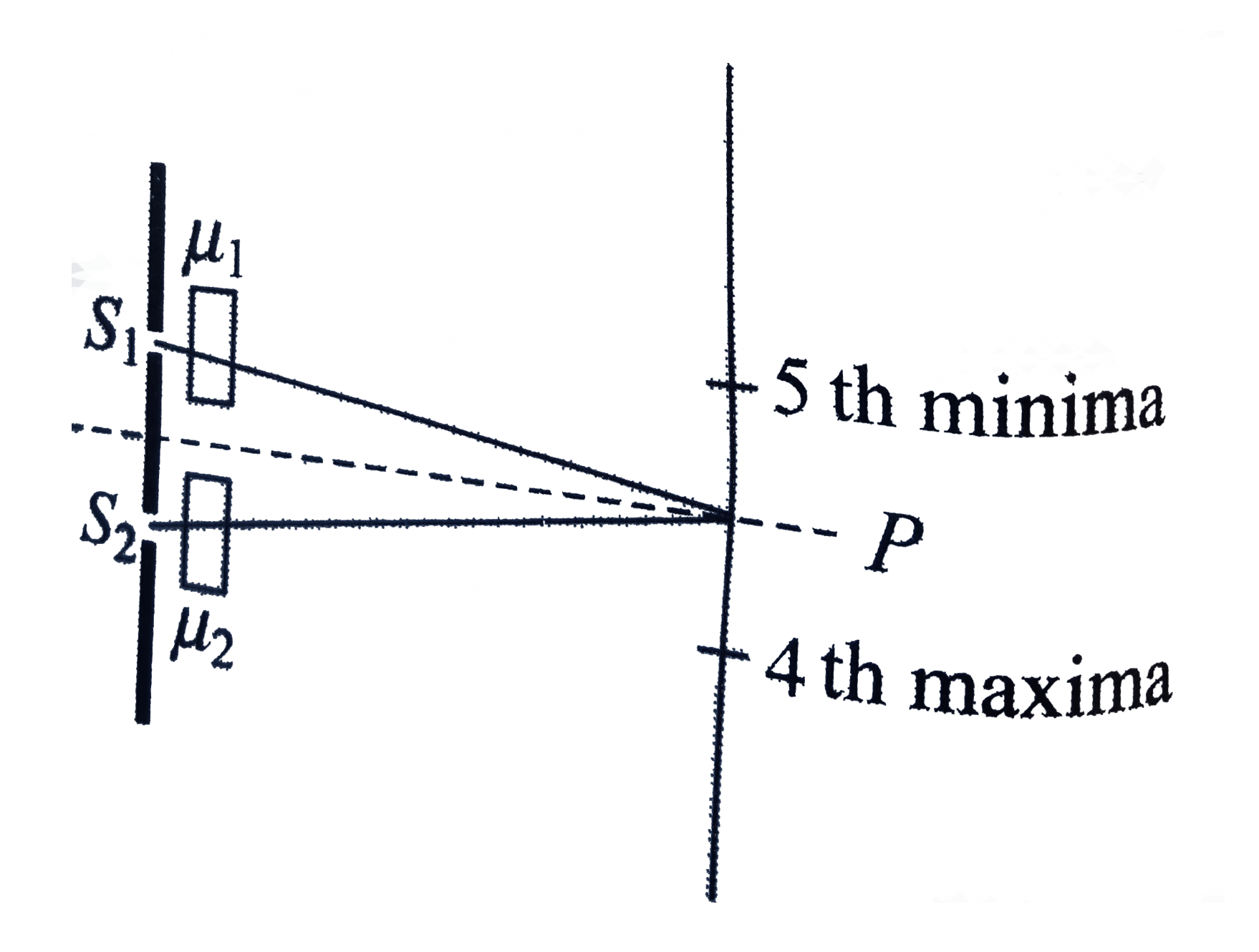
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400Å
It is found that point P on the screen where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
View Solution
