Let f(x)=∣∣∣∣x2−4x+3∣∣−2∣∣. Which of the following is/are correct ?
f(x)= m has exactly two real solutios of different sign ∀m>2
f(x)=m has exactly two real solution ∀m∈(2,∞)∪{0}
f(x)=m has no solutions ∀m<0
f(x)=m has four distinct real solution ∀m∈(0,1)
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the function f(x)=||x2−4x+3|−2| and determine the validity of the given statements regarding the solutions of the equation f(x)=m.
Step 1: Simplify the inner expression
First, we simplify the expression inside the outer absolute value.
1. The quadratic x2−4x+3 can be factored as:
x2−4x+3=(x−1)(x−3)
This quadratic has roots at x=1 and x=3.
Step 2: Analyze the quadratic
2. The quadratic opens upwards (since the coefficient of x2 is positive) and is zero at x=1 and x=3. The vertex of the parabola occurs at x=2, where:
f(2)=22−4⋅2+3=1
Thus, the minimum value of |x2−4x+3| is 0 (at x=1 and x=3) and the maximum value occurs at the vertex.
Step 3: Determine the range of the inner absolute value
3. The maximum value of |x2−4x+3| occurs at the vertex x=2:
|1|=1
Therefore, |x2−4x+3| ranges from 0 to ∞.
Step 4: Analyze the outer absolute value
4. Now we analyze ||x2−4x+3|−2|:
- For |x2−4x+3|<2 (which occurs between the roots), the expression will be negative, so we take the negative:
||x2−4x+3|−2|=2−|x2−4x+3|
- For |x2−4x+3|≥2, the expression remains positive:
||x2−4x+3|−2|=|x2−4x+3|−2
Step 5: Determine the critical points
5. The critical points occur at x=1 and x=3, where |x2−4x+3|=0. The function f(x) will equal 2 at points where the inner expression equals 2.
Step 6: Analyze the statements
Now we analyze the statements based on the graph and the behavior of f(x):
1. First Statement: f(x)=m has exactly two real solutions of different signs for all m>2.
- Correct: The graph of f(x) will intersect the horizontal line y=m at two points.
2. Second Statement: f(x)=m has exactly two real solutions for all m in (0,2).
- Correct: The function will cross the line y=m twice in this range.
3. Third Statement: f(x)=m has no solution for all m<0.
- Correct: Since f(x) is always non-negative, there are no solutions for negative m.
4. Fourth Statement: f(x)=m has exactly four distinct solutions for all m in (0,1).
- Correct: The graph will intersect the horizontal line y=m four times in this interval.
Conclusion
All statements are correct.
First, we simplify the expression inside the outer absolute value.
x2−4x+3=(x−1)(x−3)
This quadratic has roots at x=1 and x=3.
2. The quadratic opens upwards (since the coefficient of x2 is positive) and is zero at x=1 and x=3. The vertex of the parabola occurs at x=2, where:
f(2)=22−4⋅2+3=1
Thus, the minimum value of |x2−4x+3| is 0 (at x=1 and x=3) and the maximum value occurs at the vertex.
3. The maximum value of |x2−4x+3| occurs at the vertex x=2:
|1|=1
Therefore, |x2−4x+3| ranges from 0 to ∞.
4. Now we analyze ||x2−4x+3|−2|:
- For |x2−4x+3|<2 (which occurs between the roots), the expression will be negative, so we take the negative:
||x2−4x+3|−2|=2−|x2−4x+3|
- For |x2−4x+3|≥2, the expression remains positive:
||x2−4x+3|−2|=|x2−4x+3|−2
5. The critical points occur at x=1 and x=3, where |x2−4x+3|=0. The function f(x) will equal 2 at points where the inner expression equals 2.
Now we analyze the statements based on the graph and the behavior of f(x):
- Correct: The graph of f(x) will intersect the horizontal line y=m at two points.
- Correct: The function will cross the line y=m twice in this range.
- Correct: Since f(x) is always non-negative, there are no solutions for negative m.
- Correct: The graph will intersect the horizontal line y=m four times in this interval.
All statements are correct.
Topper's Solved these Questions
- FUNCTION BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - FUNCTION EXERCISE - COMPREHENSION TYPE PROBLEMS
13 Videos
- FUNCTION BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - FUNCTION EXERCISE - MATCHING TYPE PROBLEMS
6 Videos
- FUNCTION BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - FUNCTION EXERCISE - SUBJECTIVE TYPE PROBLEMS
33 Videos
- ELLIPSE BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - ELLIPSE EXERCISE - Exercise-4 : Subjective Type Problems
2 Videos
- HYPERBOLABOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise-4 : Subjective Type Problems
3 Videos
Similar Questions
Let f(x)=(x2−3x+2)(x2+3x+2)andα,β,γ satisfy α<βγ are the roots of f'(x)=0 then which of the following is/are correct ([.] denots greatest integer function) ?
View SolutionLet y=f(x) be satisfying differential equation e−x2dydx=2xy2 such that f(0)=12
Q. Which of the following statement is correct about f(x)?
View Solution
Knowledge Check
If f(x)=4x+2, which of the following is the graph of f(x)?
A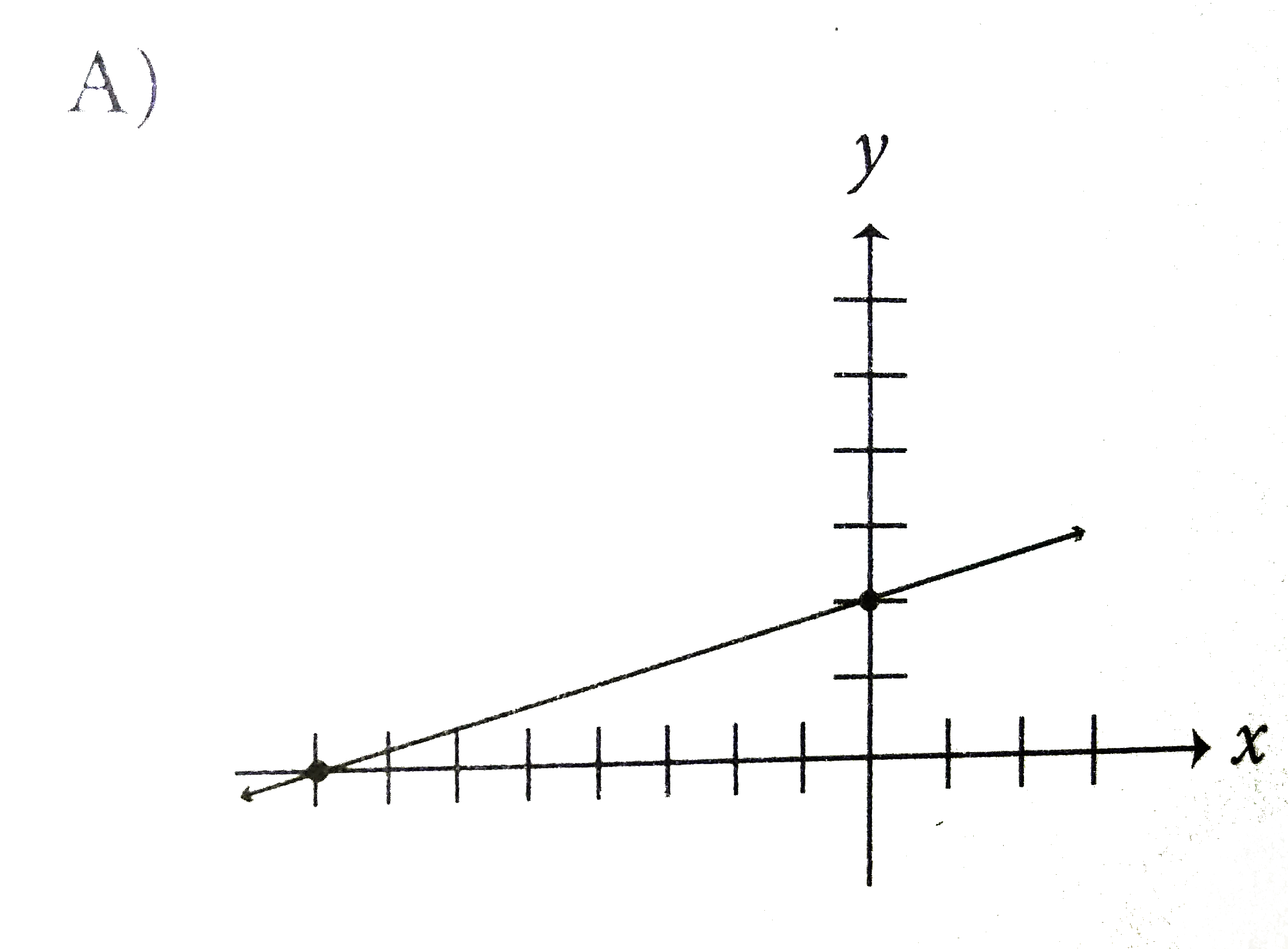 B
B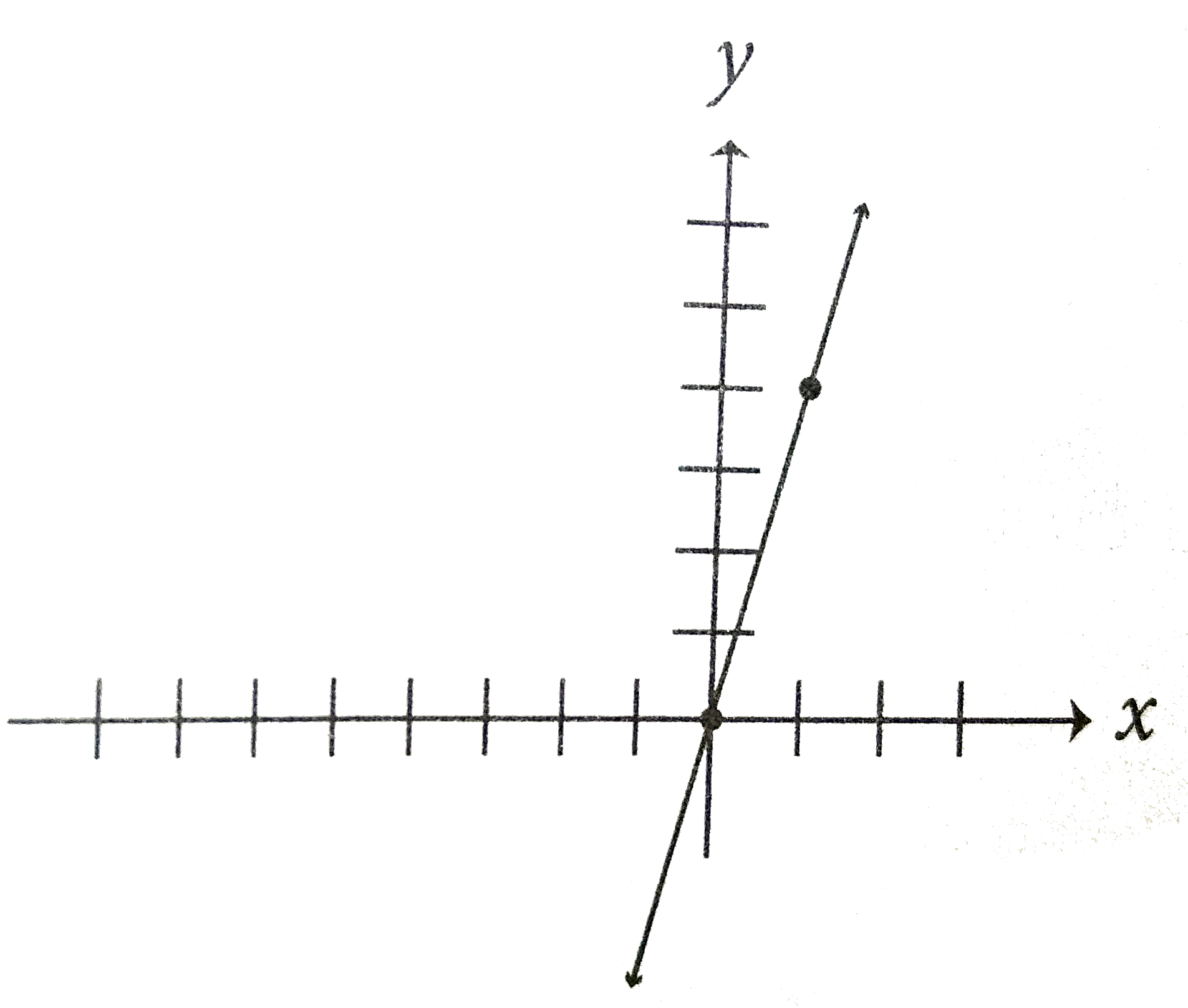 C
C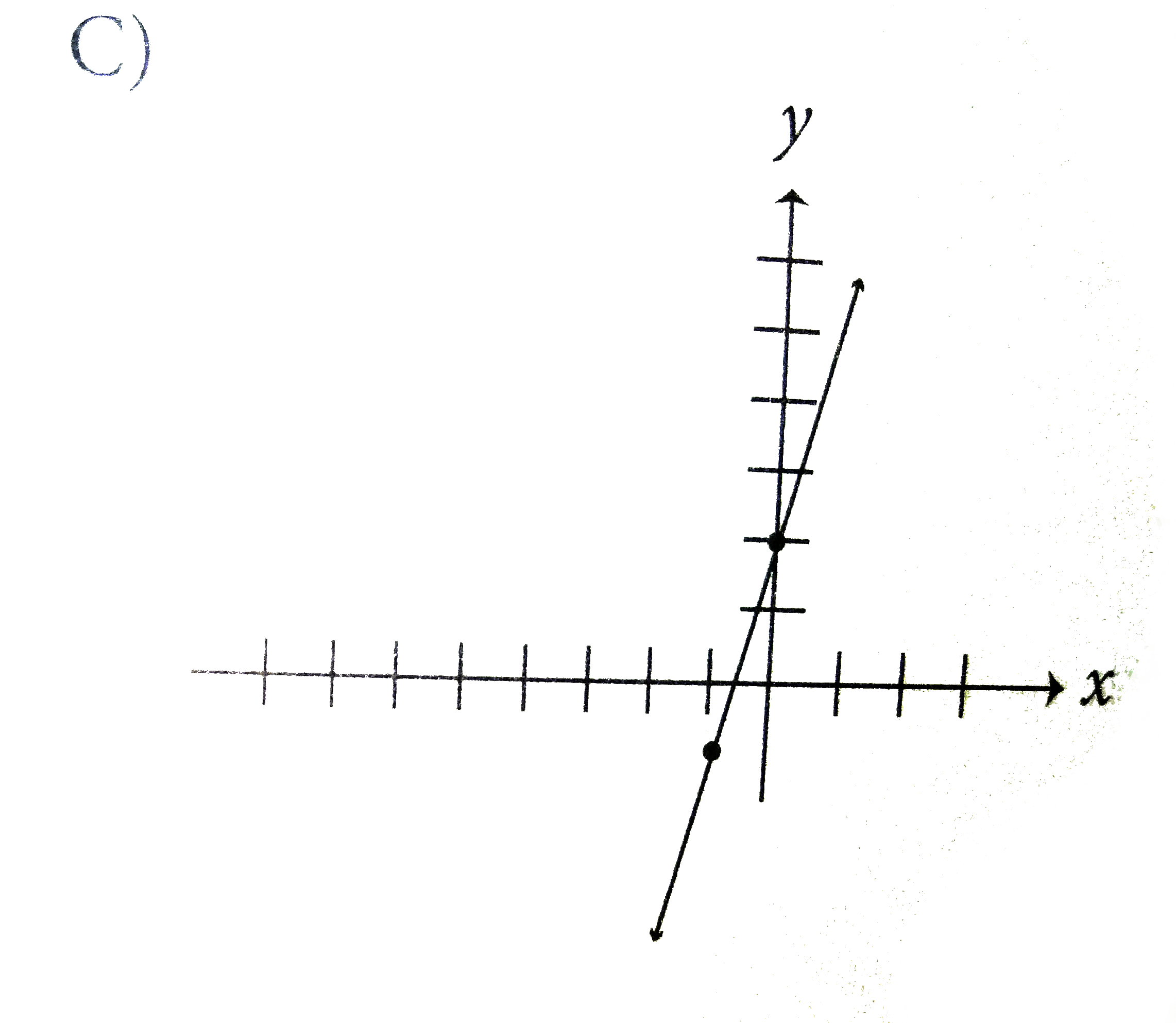 D
D
Let f(x)=sin−1xandg(x)=cos−1x, then which of the following statements are correct?
View SolutionLet f(x)=cos−1(1−tan2(x/2)1+tan2(x/2))
Which of the following statement (s) is/are correct about f(x) ?
View SolutionLet y=f(x) be satisfying differential equation e−x2dydx=2xy2 such that f(0)=12
Which of the following statements is correct about f(x)?
View SolutionLet a=sin−(sin3)+sin−1(sin4)+sin−1(sin5),f(x)=ex2+|x|, domain of f(x) be [a,∞) & range of f(x) be [b,∞) and g(x)=(4cos4x−2cos2x−14cos4x−x7)1/7, domain & range of g(x) is set of real numbers. Which of the following are correct
View SolutionLet f(x)=tan−1(√1+x2−1x) then which of the following is correct :
View SolutionLet f(x)=tan−1(√1+x2−1x) then which of the following is correct :
View SolutionLet f(x) =403x4+8x3−18x2+60. Which of the following statement (s) about f(x) is (are ) correct ?
View Solution
