Point A lies on the curve y=ex2 and has the coordinate (x,e−x2) where x>0. Point B has the coordinates (x,0). If 'O' is the origin, then the maximum area of the ΔAOB is
1√8e
1√4e
1√2e
1√e
The correct Answer is:A
To find the maximum area of triangle AOB, where point A lies on the curve y=ex2 at coordinates (x,e−x2) and point B has coordinates (x,0), we will follow these steps:
Step 1: Identify the Area of Triangle AOB
The area A of triangle AOB can be calculated using the formula for the area of a triangle:
A=12×base×height
In this case, the base is the distance from the origin O to point B, which is x, and the height is the y-coordinate of point A, which is e−x2. Therefore, the area can be expressed as:
A=12×x×e−x2
Step 2: Differentiate the Area with Respect to x
To find the maximum area, we need to differentiate A with respect to x:
A=12xe−x2
Using the product rule, we differentiate:
dAdx=12(e−x2+xddx(e−x2))
The derivative of e−x2 is −2xe−x2, so:
dAdx=12(e−x2−2x2e−x2)
This simplifies to:
dAdx=e−x22(1−2x2)
Step 3: Set the Derivative to Zero
To find the critical points, we set dAdx=0:
e−x22(1−2x2)=0
Since e−x2 is never zero, we solve:
1−2x2=0⟹2x2=1⟹x2=12⟹x=1√2
Step 4: Find the Maximum Area
Now, we substitute x=1√2 back into the area formula to find the maximum area:
A=12×1√2×e−(1√2)2=12×1√2×e−12
This simplifies to:
A=12√2×1√e=12√2e
Final Result
Thus, the maximum area of triangle AOB is:
12√2e
The area A of triangle AOB can be calculated using the formula for the area of a triangle:
A=12×base×height
In this case, the base is the distance from the origin O to point B, which is x, and the height is the y-coordinate of point A, which is e−x2. Therefore, the area can be expressed as:
A=12×x×e−x2
To find the maximum area, we need to differentiate A with respect to x:
A=12xe−x2
Using the product rule, we differentiate:
dAdx=12(e−x2+xddx(e−x2))
The derivative of e−x2 is −2xe−x2, so:
dAdx=12(e−x2−2x2e−x2)
This simplifies to:
dAdx=e−x22(1−2x2)
To find the critical points, we set dAdx=0:
e−x22(1−2x2)=0
Since e−x2 is never zero, we solve:
1−2x2=0⟹2x2=1⟹x2=12⟹x=1√2
Now, we substitute x=1√2 back into the area formula to find the maximum area:
A=12×1√2×e−(1√2)2=12×1√2×e−12
This simplifies to:
A=12√2×1√e=12√2e
Thus, the maximum area of triangle AOB is:
12√2e
Topper's Solved these Questions
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
3 Videos
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (COMPREHENSION TYPE PROBLEMS)
6 Videos
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
22 Videos
- BIONMIAL THEOREMBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - BIONMIAL THEOREMEXERCISE - Exercise-4 : Subjective Type Problems
15 Videos
Similar Questions
For the curve y=xex , the point
View SolutionFind the area bounded by the curve y=x2−2x+5, the tangent to it at the point (2,5) and the axes of the coordinates.
View SolutionPoint O has coordinates (0, 0), point P lies on the graph of y=6−x2, and point B has coordinates (2√3,0). If OP=BP, the area of triangle OPB is
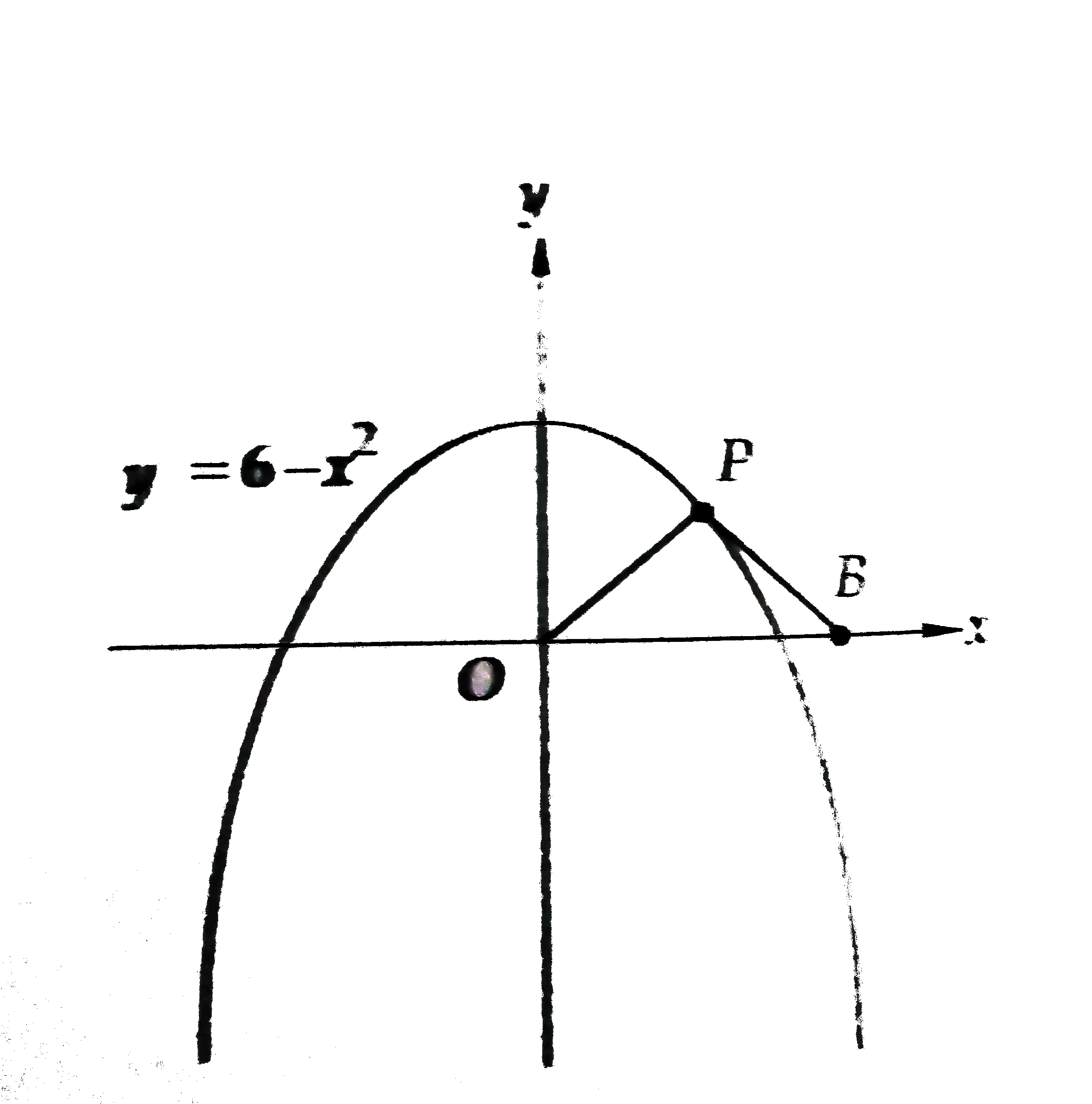
View SolutionThe coordinates of the image of the origin O with respect to the line x+y+1=0 are
View SolutionThe area bounded by the curve y=xe−x;xy=0and x=c where c is the x-coordinate of the curve's inflection point, is
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
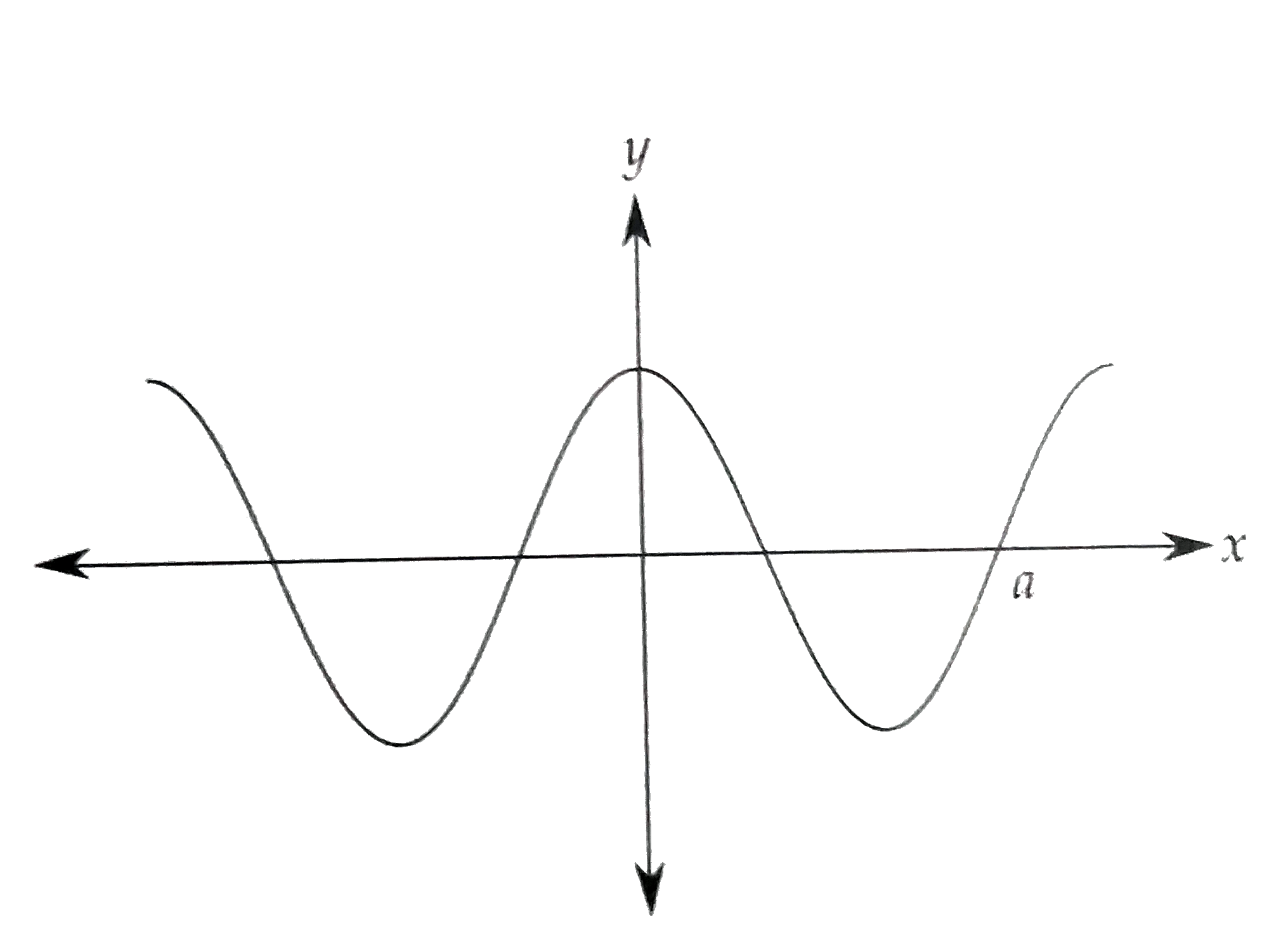
View SolutionThe graph of y=cos.x2 is shown in Figure Point a has coordinates (t, 0). What is the value of t in radians ?
View SolutionFind the slope of the tangent to the curve y=x3−3x+2 at the point whose x-coordinate is 3.
View SolutionFind the slope of the tangent to the curve y=x3−3x+2 at the point whose x-coordinate is 3.
View SolutionThe point of contact of a tangent from the point (1,2) to the circle x2+y2=1 has the coordinates :
View Solution
