The compound MX4 is tetrahedral. The number of ∠XMX angles formed in the compound is
three
four
five
six
The correct Answer is:D
To determine the number of ∠XMX angles formed in the tetrahedral compound MX4, we can follow these steps:
1. Understanding Tetrahedral Geometry:
- The compound MX4 has a tetrahedral geometry, which means that the central atom M is surrounded by four X atoms at the corners of a tetrahedron.
2. Identifying the Angles:
- In a tetrahedral structure, there are multiple angles formed between the central atom M and the surrounding atoms X. Specifically, we are interested in the angles formed between the lines connecting the central atom M to the surrounding atoms X.
3. Counting the Unique Angles:
- For a tetrahedral structure with four surrounding atoms, we can label them as X1, X2, X3, and X4. The angles formed between these atoms and the central atom M are:
- Angle between X1, M, and X2
- Angle between X1, M, and X3
- Angle between X1, M, and X4
- Angle between X2, M, and X3
- Angle between X2, M, and X4
- Angle between X3, M, and X4
4. Total Number of Angles:
- By listing all the unique combinations, we find that there are a total of 6 unique ∠XMX angles formed in the tetrahedral structure.
5. Conclusion:
- Therefore, the number of ∠XMX angles formed in the compound MX4 is 6.
Final Answer:
The number of ∠XMX angles formed in the compound MX4 is 6.
- The compound MX4 has a tetrahedral geometry, which means that the central atom M is surrounded by four X atoms at the corners of a tetrahedron.
- In a tetrahedral structure, there are multiple angles formed between the central atom M and the surrounding atoms X. Specifically, we are interested in the angles formed between the lines connecting the central atom M to the surrounding atoms X.
- For a tetrahedral structure with four surrounding atoms, we can label them as X1, X2, X3, and X4. The angles formed between these atoms and the central atom M are:
- Angle between X1, M, and X2
- Angle between X1, M, and X3
- Angle between X1, M, and X4
- Angle between X2, M, and X3
- Angle between X2, M, and X4
- Angle between X3, M, and X4
- By listing all the unique combinations, we find that there are a total of 6 unique ∠XMX angles formed in the tetrahedral structure.
- Therefore, the number of ∠XMX angles formed in the compound MX4 is 6.
The number of ∠XMX angles formed in the compound MX4 is 6.
Topper's Solved these Questions
- CHEMICAL BONDING (BASIC)BOOK - VK JAISWAL ENGLISHCHAPTER - CHEMICAL BONDING (BASIC)EXERCISE - Level 2
62 Videos
- CHEMICAL BONDING (BASIC)BOOK - VK JAISWAL ENGLISHCHAPTER - CHEMICAL BONDING (BASIC)EXERCISE - Level 3 (Passive 1)
6 Videos
- CHEMICAL BONDING (ADVANCED)BOOK - VK JAISWAL ENGLISHCHAPTER - CHEMICAL BONDING (ADVANCED)EXERCISE - SUBJECTIVE PROBLEMS
64 Videos
- CO-ORDINATION COMPOUNDSBOOK - VK JAISWAL ENGLISHCHAPTER - CO-ORDINATION COMPOUNDSEXERCISE - LEVEL 2
144 Videos
Similar Questions
Knowledge Check
The number of all the possible stereoisomers formed by the given compound is :
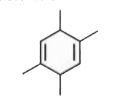 A2B3C32D64
A2B3C32D64Total number of stereoisomers of the compound 2-4-dichloroheptane is:
A0B1C2D3
Alkali metals forms following compound
View Solutionwhich forms interstitial compounds?
View SolutionA mineral MX2 crystallizes in ccp of M2+ ions whereas X− ions occupy the tetrahedral voids. The number of cations and anions per unit cell, the coordination number of cation and percent of tetrahedral voids occupied are :
View SolutionThe compound AgF2 is an unstable compound. However, if formed, the compound acts as a strong oxidising agent. Why?
View SolutionThe correct IUPAC numbering in the compound
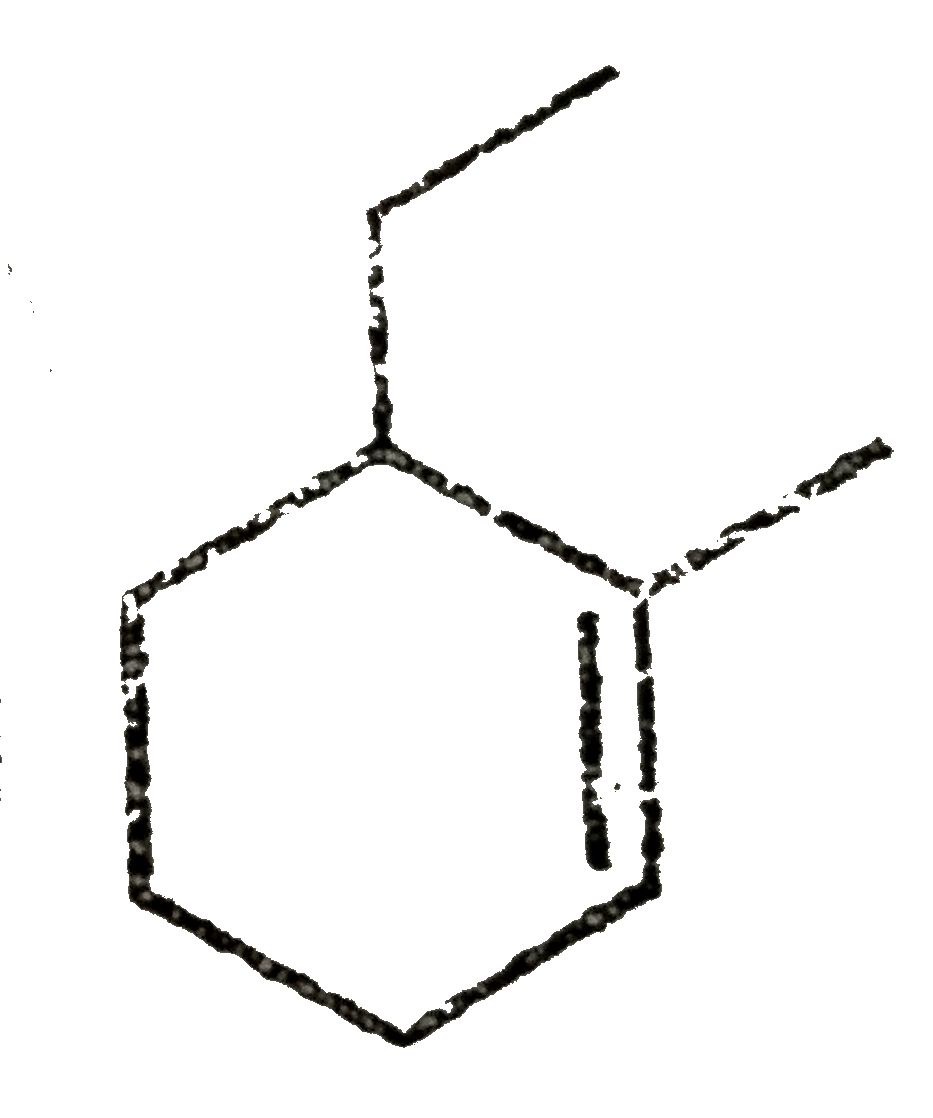 is:
is:
View SolutionWhy Be generally form covalent compounds?
View Solution
