Let m and n be positive integers and x,y>0andx+y=k, where k is constant. Let f(x,y)=xmyn, then: (a) f(x,y) is maximum when x=mkm+n (b) f(x,y) is maximuim where x=y (c) maximum value of f(x,y) is mnnmkm+n(m+n)m+n (d) maximum value of f(x,y) is km+nmmnn(m+n)m+n
f(x,y) is maximum when x=mkm+n
f(x,y) is maximuim wheere x=y
maximum value of f(x,y)ismnnmkm+n(m+n)m+n
maximum vlaue of f(x,y)iskm+nmmnn(m+n)m+n
The correct Answer is:A, D
To solve the problem, we need to find the maximum value of the function f(x,y)=xmyn given the constraint x+y=k. We will use the method of substitution and differentiation to find the maximum value.
Step 1: Substitute for y
Since we have the constraint x+y=k, we can express y in terms of x:
y=k−x
Step 2: Rewrite the function
Now, substitute y into the function f(x,y):
f(x)=xm(k−x)n
Step 3: Differentiate f(x)
To find the maximum, we need to differentiate f(x) with respect to x and set the derivative equal to zero:
f′(x)=ddx(xm(k−x)n)
Using the product rule, we have:
f′(x)=mxm−1(k−x)n+xm⋅n(k−x)n−1(−1)
This simplifies to:
f′(x)=mxm−1(k−x)n−nxm(k−x)n−1
Step 4: Set the derivative to zero
Setting f′(x)=0:
mxm−1(k−x)n=nxm(k−x)n−1
Step 5: Factor out common terms
We can factor out xm−1(k−x)n−1:
xm−1(k−x)n−1(m(k−x)−nx)=0
Since x>0 and k−x>0, we can ignore the first factor, leading to:
m(k−x)−nx=0
Step 6: Solve for x
Rearranging gives:
mk−mx=nx
Combining terms:
mk=(m+n)x
Thus,
x=mkm+n
Step 7: Find y
Using y=k−x:
y=k−mkm+n=nkm+n
Step 8: Maximum value of f(x,y)
Now we substitute x and y back into the function to find the maximum value:
f(mkm+n,nkm+n)=(mkm+n)m(nkm+n)n
This simplifies to:
=mmnnkm+n(m+n)m+n
Conclusion
Thus, the maximum value of f(x,y) is:
mmnnkm+n(m+n)m+n
Final Answers
- (a) f(x,y) is maximum when x=mkm+n is True.
- (b) f(x,y) is maximum where x=y is False.
- (c) Maximum value of f(x,y) is (mnnmkm+n)(m+n)m+n is False.
- (d) Maximum value of f(x,y) is km+nmmnn(m+n)m+n is True.
- (b) f(x,y) is maximum where x=y is False.
- (c) Maximum value of f(x,y) is (mnnmkm+n)(m+n)m+n is False.
- (d) Maximum value of f(x,y) is km+nmmnn(m+n)m+n is True.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - VK JAISWAL ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)
15 Videos
- APPLICATION OF DERIVATIVES BOOK - VK JAISWAL ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (MATCHING TYPE PROBLEMS)
5 Videos
- APPLICATION OF DERIVATIVES BOOK - VK JAISWAL ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
22 Videos
- AREA UNDER CURVESBOOK - VK JAISWAL ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
8 Videos
Similar Questions
A function f is defined by f(x)=|x|m|x−1|n∀x∈R. The local maximum value of the function is (m,n∈N) (a) 1 (b) mn.nm (c)mmnn(m+n)m+n (d) (mn)mn(m+n)m+n
View SolutionIf m and n are positive integers, then prove that the coefficients of xm and xn are equal in the expansion of (1+x)m+n
View SolutionIf are positive integers, maximum value of xm(a−x)n in (0,a) is :
View SolutionIf (x−a)2m(x−b)2n+1, where mandn are positive integers and a>b, is the derivative of a function f then-
View SolutionIf (x−a)2m(x−b)2n+1, where mandn are positive integers and a>b, is the derivative of a function f then-
View SolutionLet x, y be positive real numbers and m, n be positive integers, The maximum value of the expression
xmyn(1+x2m)(1+y2n) is
View SolutionIf xandy are positive real numbers and m,n are any positive integers, then prove that xnym(1+x2n)(1+y2m)<14
View Solutionin (M)=x
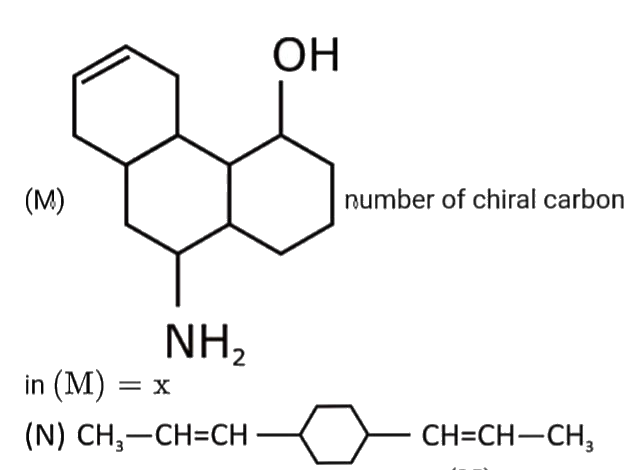
(Number of Geometrial isomers in (N)=y). The value of yx is
View SolutionIf x,y are positive real numbers and m, n are positive integers, then prove that xnym(1+x2n)(1+y2m)≤14
View SolutionThe minimum value of the fuction f(x) given by f(x)=xmm+x−nn where 1m+1n=1 and m>1 is
View Solution
