A conical vessel is to be prepared out of a circular sheet of metal of unit radius in order that the vessel has maximum value, the sectorial area that must be removed from the sheet is A1 and the area of the given sheet is A2, then A2A1 is equal to
The correct Answer is:9
To solve the problem, we need to find the ratio A2A1, where A2 is the area of the circular sheet of metal and A1 is the sectorial area that must be removed to form a conical vessel with maximum volume.
Step 1: Define the areas
1. Area of the circular sheet A2:
The area A2 of a circle with radius 1 is given by:
A2=πr2=π(12)=π
2. Sectorial area A1:
The sectorial area A1 that must be removed is related to the angle θ of the sector. The formula for the area of a sector is:
A1=12r2θ
Since the radius r is 1, we have:
A1=12(12)θ=12θ
Step 2: Relate the angle θ to the cone's dimensions
To form the cone, we need to relate the angle θ to the radius rc of the cone's base and its height h.
Using the Pythagorean theorem in the right triangle formed by the radius of the cone, the height, and the slant height (which is the radius of the original circle, equal to 1):
12=r2c+h2⟹r2c=1−h2
Step 3: Find the volume of the cone
The volume V of the cone is given by:
V=13πr2ch=13π(1−h2)h
Step 4: Maximize the volume
To find the maximum volume, we differentiate V with respect to h and set the derivative to zero:
dVdh=π3(1−3h2)=0
Solving for h:
1−3h2=0⟹h2=13⟹h=1√3
Step 5: Find rc
Substituting h back to find rc:
r2c=1−h2=1−13=23⟹rc=√23
Step 6: Find the angle θ
The arc length AB of the sector is equal to the circumference of the base of the cone:
Arc length=2πrc=2π√23
Since the arc length is also given by rθ where r=1:
θ=2π√23
Step 7: Calculate A1
Substituting θ into the formula for A1:
A1=12θ=12(2π√23)=π√23
Step 8: Find the ratio A2A1
Now we can find the ratio:
A2A1=ππ√23=1√23=√32=√3√2
Thus, the final answer is:
A2A1=√3√2
The area A2 of a circle with radius 1 is given by:
A2=πr2=π(12)=π
The sectorial area A1 that must be removed is related to the angle θ of the sector. The formula for the area of a sector is:
A1=12r2θ
Since the radius r is 1, we have:
A1=12(12)θ=12θ
12=r2c+h2⟹r2c=1−h2
V=13πr2ch=13π(1−h2)h
dVdh=π3(1−3h2)=0
Solving for h:
1−3h2=0⟹h2=13⟹h=1√3
r2c=1−h2=1−13=23⟹rc=√23
Arc length=2πrc=2π√23
Since the arc length is also given by rθ where r=1:
θ=2π√23
A1=12θ=12(2π√23)=π√23
A2A1=ππ√23=1√23=√32=√3√2
A2A1=√3√2
Topper's Solved these Questions
Similar Questions
A conical vessel is to be prepared out of a circular sheet of gold of unit radius. How much sectorial area is to be removed from the sheet so that the vessel has maximum volume?
View SolutionIf A1,A2 are between two numbers, then A1+A2H1+H2 is equal to
View SolutionA metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
View SolutionIf the sequence (an) is in GP, such that a4/a6=1/4anda2+a5=216, then a1 is equal to
View SolutionGiven that a4+a8+a12+a16=224, the sum of the first nineteen terms of the arithmetic progression
a1,a2,a3,…. is equal to
View SolutionFind a1anda9 if an is given by an=n2n+1
View SolutionThe spectra of a black body at temperatures 273∘C and 546∘C are shown in the figure. If A1 and A2 be area under the two curves respectively, the value of A2A1 is
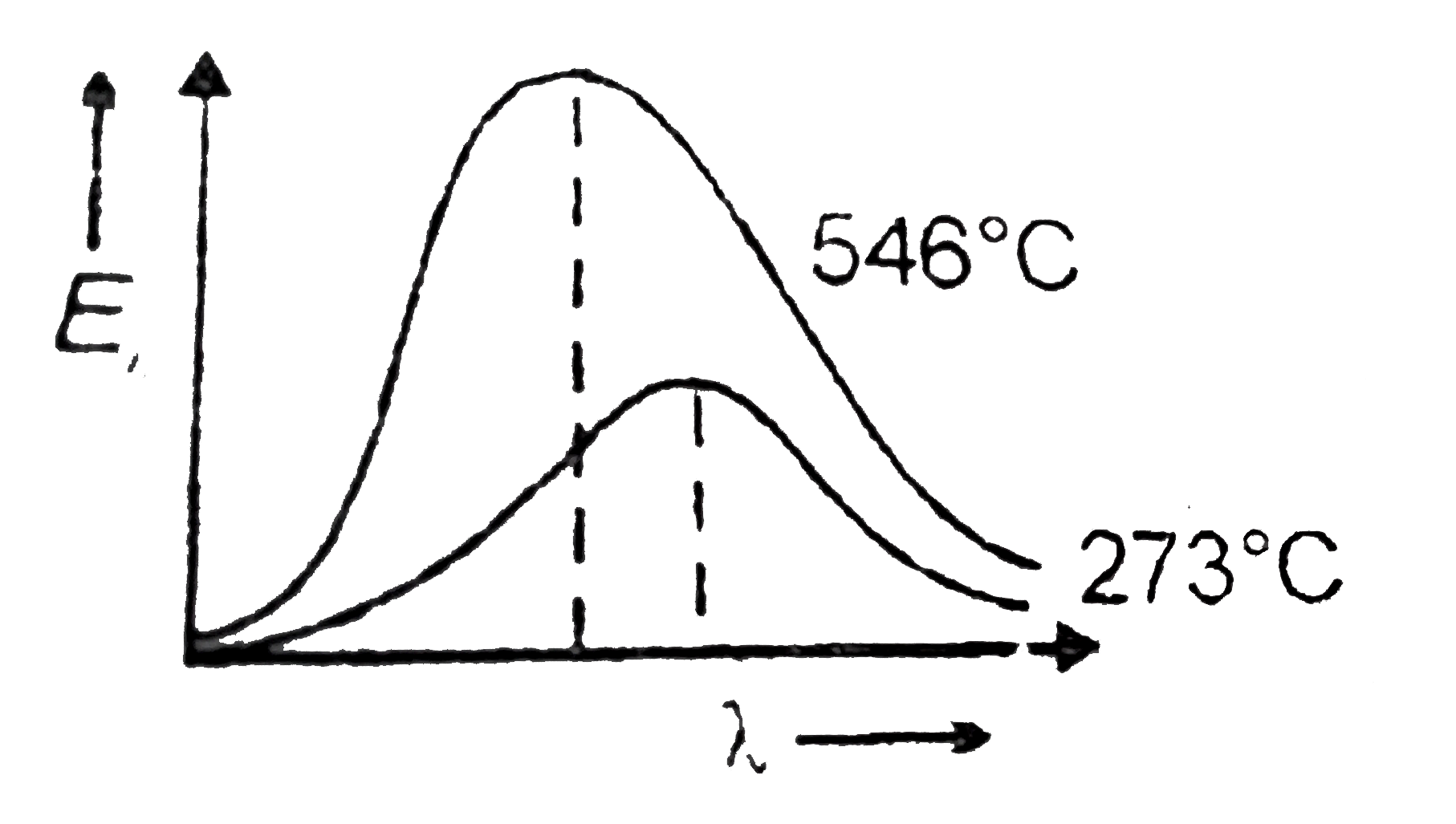
View SolutionA vessel in the form of a truncated cone has base area a1 and top area a2. It is filled to the brim with a liquid. The force at the bottom of the vessel is
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
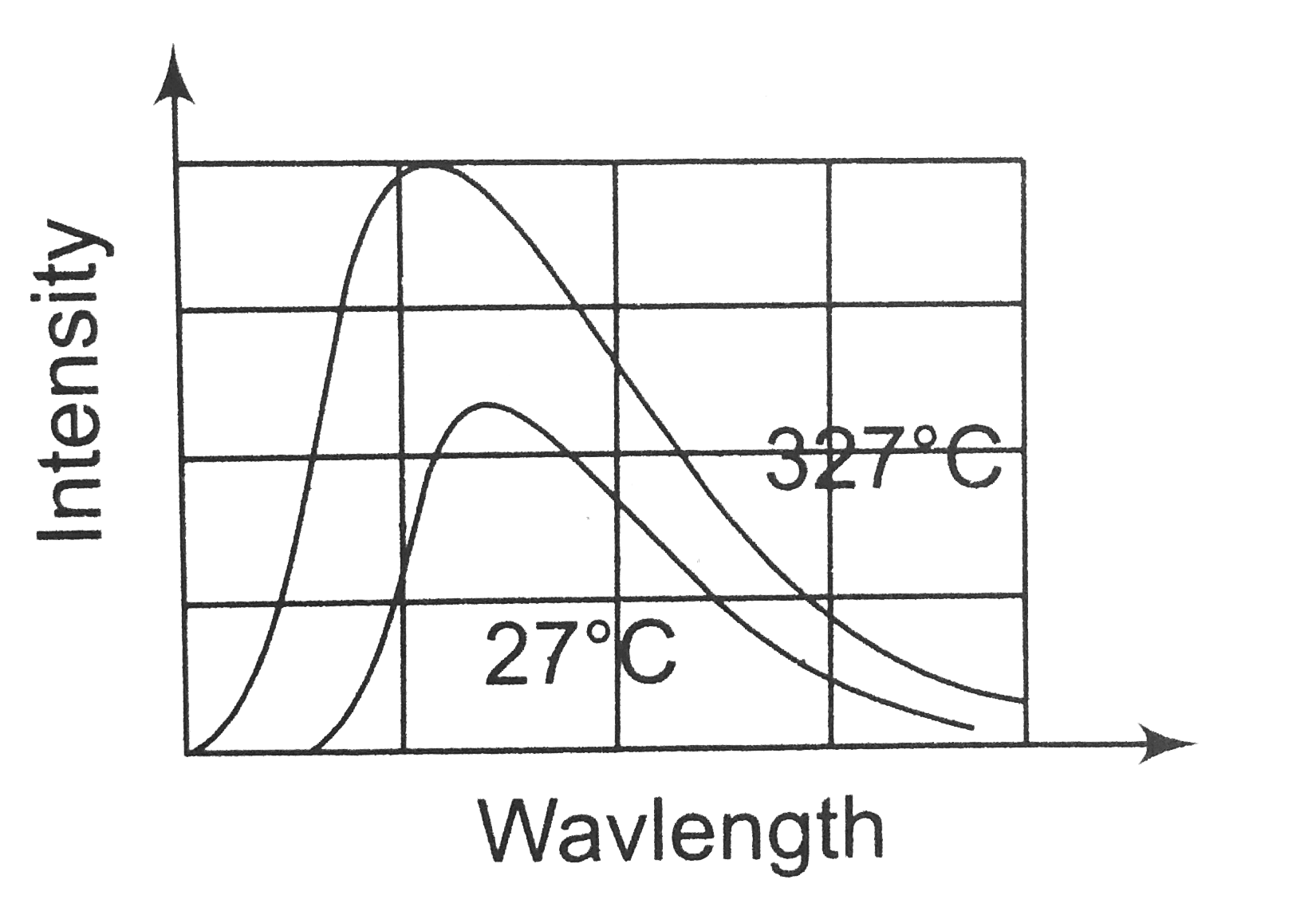
View SolutionIf a1+a5+a10+a15+a20=225, then the sum of the first 24 terms of the arithmetic progression a1,a2,a3…….. is equal to
View Solution